Solveeit Logo
Login

Question

Question: . The \(10\) Kg block is moving to the left with a speed of \(1.2\,m{s^{ - 1}}\)at time \(t = 0\). A...

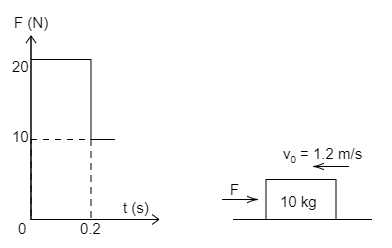
. The 1010 Kg block is moving to the left with a speed of 1.2 ms−11.2\,m{s^{ - 1}}at time t=0t = 0. A force F is applied as shown in the graph. After 0.2s0.2sthe force continues at the 10N10Nlevel. If the coefficient of Kinetic friction is μk=0.2{\mu _k} = 0.2. Determine the time t at which the block comes to stop (g=10 ms−2)\left( {g = 10\,m{s^{ - 2}}} \right)
(A) 0.333s
(B) 0.526s
(C) 0.165s
(D) None of the above.

Explanation

Solution

Hint In the question, kinetic friction, mass of the block is given. By using the formula of the equations of motion, we get the value of the time tt at which the block comes to stop has been calculated.

Formula used:
The expression for finding the time is,
v=u+atv = u + at
Where,
vv be the final velocity, uu be the initial velocity, aa be the acceleration due to the gravity and tt be the time.

Complete step by step solution:
Given that
Kinetic friction, μk=0.2{\mu _k} = 0.2
Mass of the block m=10 kgm = 10\,kg
Acceleration due to gravity g=10 ms−2g = 10\,m{s^{ - 2}}
If the block moves left, frictional force acts on the block. So, the frictional force acts towards right which means it moves towards the direction of the external force applied.
Friction force f=μkmgf = {\mu _k}mg
Substitute the known values in the above equation, we get
f=0.2×10×10f = 0.2 \times 10 \times 10
Performing the arithmetic operations in the above equation, we get
f=20 Nf = 20\,N
Force is applied for the duration of 0⩽t⩽0.2 s0 \leqslant t \leqslant 0.2\,s
External force F=20 NF = 20\,N
Total force acting on the block F′=F+fF' = F + f
Substitute the known values in the above equation, we get
F′=20+20F' = 20 + 20
Perform the arithmetic operation, we get
F′=40 NF' = 40\,N
Retardation of block a=−F′ma = - \dfrac{{F'}}{m}
Substitute the known values in the above equation, we get
a=−4010a = \dfrac{{ - 40}}{{10}}
Simplify the above equation, we get
a=−4 ms−2a = - 4\,m{s^{ - 2}}
Velocity of the block after 0.2 s0.2\,s, we get
v=u+atv = u + at Here, t=0.2 st = 0.2\,s
Substitute the known values in the above equation, we get
v=1.2−4×0.2v = 1.2 - 4 \times 0.2
Simplify the above equation we get
v=0.4 ms−2(towards left)v = 0.4\,m{s^{ - 2}}\left( {{\text{towards left}}} \right)
For the duration above t⩾0.2 st \geqslant 0.2\,s
External force F=10 NF = 10\,N
Total force acting on the block F′=F+fF' = F + f
F′=10+20F' = 10 + 20
Perform the arithmetic operation, we get
F′=30NF' = 30N
Retardation of the block a=−F′ma = - \dfrac{{F'}}{m}
a=−3010a = \dfrac{{ - 30}}{{10}}
Simplify the above equation, we get
a=−3 ms−2a = - 3\,m{s^{ - 2}}
Let the time reaches, after it comes to rest
So therefore v′=0v' = 0
v′=u+at′v' = u + at'
Substitute the known values in the above equation, we get
0=0.4−3t′0 = 0.4 - 3t'
t′=0.133 st' = 0.133\,s
Therefore, the total time after which the block comes to rest T=t+t′T = t + t'
T=0.2+0.133T = 0.2 + 0.133
T=0.333 sT = 0.333\,s.
Therefore, the time after it comes to stop is 0.333 s.0.333\,s.

Hence, from the above options option A is correct.

Note: In the question the value of the time is given. By finding the difference of the before and after timing. Substitute those values in the equation of motions and find the difference of the value of the time, after it comes to rest. Then we get the value of the time.