Question

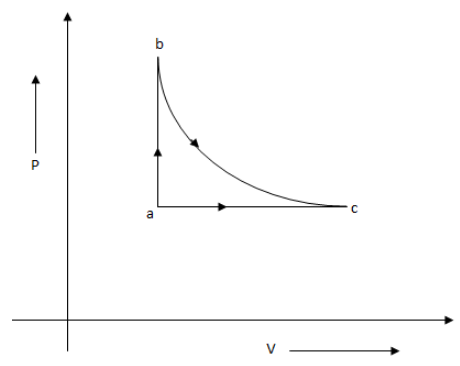
The $0.2$ moles of an ideal gas is taken around the cycle abc as shown in the figure. The path b-c is adiabatic process, a-b is isovolumic process and c-a is isobaric process. The temperature at a and b are ${T_a} = 300\,{\text{K}}$ and ${T_b} = 500\,{\text{K}}$ and pressure at a is ${\text{1}}$ atmosphere. Find the volume at c.
( Given $\gamma = \dfrac{{{C_p}}}{{{C_v}}} = \dfrac{5}{3}$ , $R = 8.205 \times {10^{ - 2}}\,{\text{L atm mo}}{{\text{l}}^{ - 1}}\,{{\text{K}}^{ - 1}}$ )

A. $6.9{\text{ L}}$
B. $6.68{\text{ L}}$
C. ${\text{5}}{\text{.52 L}}$
D. ${\text{5}}{\text{.82 L}}$

Answer 1

We are asked to find the volume at point c. To find the volume at point c, we need to find the pressure and volume at point b. Here, you will need to use Gay-Lussac’s law to find the pressure at point b and use ideal gas equation to find the volume at point b. Then use the equation for the adiabatic process to find the volume at point c.

Complete step by step answer:
Given, number of moles, $n = 0.2$.
The path b-c is adiabatic process, a-b is isovolumic process and a-c is isobaric process.
The temperature at point a, ${T_a} = 300\,{\text{K}}$.
The temperature at point b, ${T_b} = 500\,{\text{K}}$.
Pressure at point a, ${P_a} = 1{\text{ atm}}$.
Ratio of specific heats, $\gamma = \dfrac{{{C_p}}}{{{C_v}}} = \dfrac{5}{3}$.
Gas constant, $R = 8.205 \times {10^{ - 2}}\,{\text{L atm mo}}{{\text{l}}^{ - 1}}\,{{\text{K}}^{ - 1}}$.
Let the pressure at point b and c be ${P_b}$ and ${P_c}$ respectively.
Let the volume at point b and c be ${V_b}$ and ${V_c}$ respectively.

The path a-b is an isovolumic process, which means the volume is constant for path a-b.
According to Gay-Lussac’s law when volume is constant for an ideal gas, we can write
$\dfrac{P}{T} = {\text{constant}}$
Applying Gay-Lussac’s law for path a-b we get,
$\dfrac{{{P_a}}}{{{T_a}}} = \dfrac{{{P_b}}}{{{T_b}}}$
Putting the values of ${P_a}$, ${T_a}$ and ${T_b}$ we get,
$\dfrac{1}{{300}} = \dfrac{{{P_b}}}{{500}}$
$\Rightarrow \dfrac{{{P_b}}}{{500}} = \dfrac{1}{{300}}$
$\Rightarrow {P_b} = \dfrac{5}{3}\,\,{\text{atm}}$

From ideal gas equation we have,
$PV = nRT$
where $P$ is the pressure, $V$ is the volume, $n$ is the number of moles, $R$ is gas constant and $T$ is temperature.
Using ideal gas equation at point b we get,
${P_b}{V_b} = nR{T_b}$
Putting the values of ${P_b}$, $n$, $R$ and ${T_b}$ we get,
$\dfrac{5}{3}\,{V_b} = 2 \times 8.205 \times {10^{ - 2}} \times 500$
$\Rightarrow \,{V_b} = \dfrac{3}{5} \times 2 \times 8.205 \times {10^{ - 2}} \times 500$
$\Rightarrow \,{V_b} = 4.92\,{\text{L}}$

The path b-c is an adiabatic process.
For adiabatic process we have the equation,
$P{V^\gamma } = {\text{constant}}$
where $P$ is the pressure, $V$ is the volume and $\gamma$ is ratio of specific heats.
Using this equation for path b-c we get,
${P_b}{V_b}^\gamma = {P_c}{V_c}^\gamma$ (i)
From the graph, we get ${P_c} = {P_a} = 1\,{\text{atm}}$.
Now, putting the values of ${P_b}$, ${V_b}$, ${P_c}$ and $\gamma$ in equation (i) we get,
$\dfrac{5}{3} \times {4.92^{\dfrac{5}{3}}} = 1 \times {V_c}^{\dfrac{5}{3}}$
$\Rightarrow {V_c} = {\left( {\dfrac{5}{3} \times {{4.92}^{\dfrac{5}{3}}}} \right)^{\dfrac{3}{5}}}$
$\Rightarrow {V_c} = {\dfrac{5}{3}^{^{\dfrac{3}{5}}}} \times 4.92$
$\therefore {V_c} = 6.68\,{\text{L}}$
Therefore, the volume at c is $6.68\,{\text{L}}$

Hence, the correct answer is option B.

Note: There are four gas laws which are important to remember, these are
1. Boyle’s law:- Boyle’s law states that when temperature is constant, then pressure of the gas is inversely proportional to its volume.
2. Charles’s law:- Charles’ law states that volume occupied by a gas is proportional to the temperature of the gas at constant pressure.
3. Avogadro’s law:- Avogadro’s law states that different gases of equal volume contain equal numbers of moles at same temperature and pressure.
4. Gay-Lussac’s law:- Gay-Lussac’s law states that for constant volume, pressure is directly proportional to the temperature of the gas.