Question

$\text{(III)}$

$x=\sqrt{7-3i}$

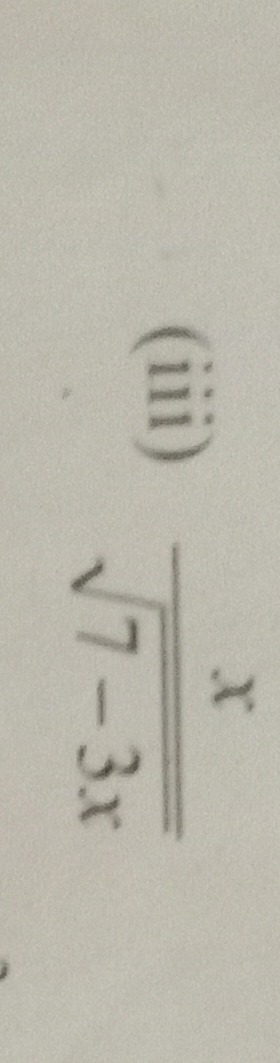
Answer 1

$$x=\pm\left(\sqrt{\frac{7+\sqrt{58}}{2}}- i\sqrt{\frac{\sqrt{58}-7}{2}}\right)$$

Answer 2

We write

$$x=\sqrt{7-3i}=a+bi,\quad a,b\in\mathbb{R}.$$

Then,

$$(a+bi)^2= a^2-b^2+2abi=7-3i.$$

By equating the real and imaginary parts we get:

$$a^2-b^2=7,\quad 2ab=-3.$$

A standard method is to use the formulas:

$$a = \sqrt{\frac{|z|+ \Re z}{2}},\quad b =-\sqrt{\frac{|z|-\Re z}{2}},$$

(since the imaginary part of $7-3i$ is negative). Here,

$$|7-3i|=\sqrt{7^2+(-3)^2}=\sqrt{49+9}=\sqrt{58}.$$

Thus,

$$a = \sqrt{\frac{\sqrt{58}+7}{2}},\quad b = -\sqrt{\frac{\sqrt{58}-7}{2}}.$$

Therefore, the two square roots are

$$x=\pm\left(\sqrt{\frac{7+\sqrt{58}}{2}}- i\sqrt{\frac{\sqrt{58}-7}{2}}\right).$$

Explanation (minimal):

1. Let $\sqrt{7-3i} = a+bi$.

2. Equate $(a+bi)^2=7-3i$ to get $a^2-b^2=7$ and $2ab=-3$.

3. Use formulas $a=\sqrt{\frac{|z|+7}{2}}$ and $b=-\sqrt{\frac{|z|-7}{2}}$ with $|z|=\sqrt{58}$.

4. Write final answer as $\pm \left(\sqrt{\frac{7+\sqrt{58}}{2}}- i\sqrt{\frac{\sqrt{58}-7}{2}}\right)$.