Solveeit Logo
Login

Question

Question: $\text{II} \circled{1}, \int_{0.5}^{1}\frac{dx}{1+e^x}$...

II\circled1,∫0.51dx1+ex\text{II} \circled{1}, \int_{0.5}^{1}\frac{dx}{1+e^x}

Answer

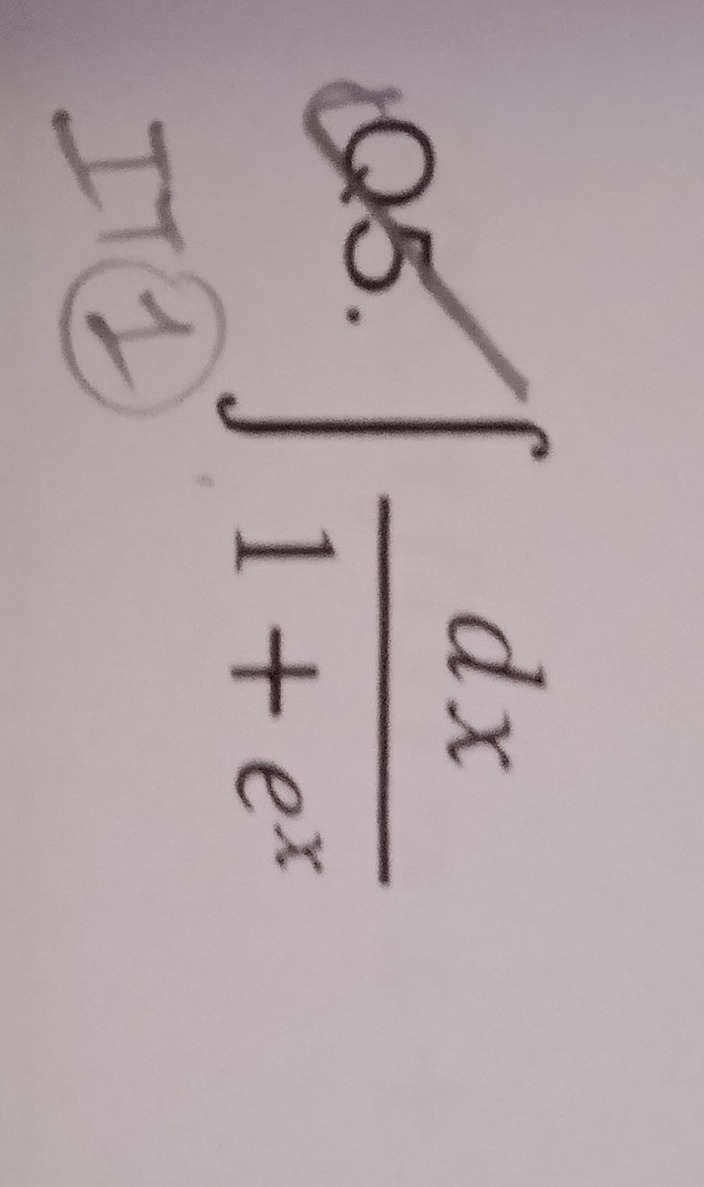
0.5 + ln((1+√e)/(1+e))

Explanation

Solution

The problem asks to evaluate the definite integral ∫0.51dx1+ex\int_{0.5}^{1}\frac{dx}{1+e^x}.

First, we find the indefinite integral ∫dx1+ex\int \frac{dx}{1+e^x}. Let I=∫dx1+exI = \int \frac{dx}{1+e^x}. We can use a substitution method or algebraic manipulation.

Method 1: Algebraic Manipulation Multiply the numerator and denominator by e−xe^{-x}: I=∫e−xdxe−x(1+ex)=∫e−xdxe−x+1I = \int \frac{e^{-x} dx}{e^{-x}(1+e^x)} = \int \frac{e^{-x} dx}{e^{-x}+1} Let u=e−x+1u = e^{-x}+1. Then du=−e−xdxdu = -e^{-x} dx, which means e−xdx=−due^{-x} dx = -du. Substitute these into the integral: I=∫−duu=−ln⁡∣u∣+CI = \int \frac{-du}{u} = -\ln|u| + C Substitute back u=e−x+1u = e^{-x}+1: I=−ln⁡(e−x+1)+CI = -\ln(e^{-x}+1) + C Simplify the expression: I=−ln⁡(1ex+1)+C=−ln⁡(1+exex)+CI = -\ln\left(\frac{1}{e^x}+1\right) + C = -\ln\left(\frac{1+e^x}{e^x}\right) + C Using logarithm properties ln⁡(a/b)=ln⁡a−ln⁡b\ln(a/b) = \ln a - \ln b: I=−(ln⁡(1+ex)−ln⁡(ex))+CI = -(\ln(1+e^x) - \ln(e^x)) + C I=−ln⁡(1+ex)+ln⁡(ex)+CI = -\ln(1+e^x) + \ln(e^x) + C Since ln⁡(ex)=x\ln(e^x) = x: I=x−ln⁡(1+ex)+CI = x - \ln(1+e^x) + C

Method 2: Substitution and Partial Fractions Let t=ext = e^x. Then dt=exdxdt = e^x dx, so dx=dtex=dttdx = \frac{dt}{e^x} = \frac{dt}{t}. Substitute these into the integral: I=∫11+t⋅dtt=∫1t(1+t)dtI = \int \frac{1}{1+t} \cdot \frac{dt}{t} = \int \frac{1}{t(1+t)} dt Decompose the integrand using partial fractions: 1t(1+t)=At+B1+t\frac{1}{t(1+t)} = \frac{A}{t} + \frac{B}{1+t} Multiply by t(1+t)t(1+t): 1=A(1+t)+Bt1 = A(1+t) + Bt. Set t=0  ⟹  1=A(1)  ⟹  A=1t=0 \implies 1 = A(1) \implies A=1. Set t=−1  ⟹  1=B(−1)  ⟹  B=−1t=-1 \implies 1 = B(-1) \implies B=-1. So, 1t(1+t)=1t−11+t\frac{1}{t(1+t)} = \frac{1}{t} - \frac{1}{1+t}. Now integrate: I=∫(1t−11+t)dt=ln⁡∣t∣−ln⁡∣1+t∣+CI = \int \left(\frac{1}{t} - \frac{1}{1+t}\right) dt = \ln|t| - \ln|1+t| + C Substitute back t=ext = e^x: I=ln⁡(ex)−ln⁡(1+ex)+CI = \ln(e^x) - \ln(1+e^x) + C I=x−ln⁡(1+ex)+CI = x - \ln(1+e^x) + C

Now, we evaluate the definite integral using the limits 0.50.5 and 11: ∫0.51dx1+ex=[x−ln⁡(1+ex)]0.51\int_{0.5}^{1}\frac{dx}{1+e^x} = [x - \ln(1+e^x)]_{0.5}^{1} Apply the limits: =(1−ln⁡(1+e1))−(0.5−ln⁡(1+e0.5))= (1 - \ln(1+e^1)) - (0.5 - \ln(1+e^{0.5})) =(1−ln⁡(1+e))−(0.5−ln⁡(1+e))= (1 - \ln(1+e)) - (0.5 - \ln(1+\sqrt{e})) =1−ln⁡(1+e)−0.5+ln⁡(1+e)= 1 - \ln(1+e) - 0.5 + \ln(1+\sqrt{e}) Combine the constant terms and logarithm terms: =(1−0.5)+(ln⁡(1+e)−ln⁡(1+e))= (1 - 0.5) + (\ln(1+\sqrt{e}) - \ln(1+e)) =0.5+ln⁡(1+e1+e)= 0.5 + \ln\left(\frac{1+\sqrt{e}}{1+e}\right)

The final answer is 0.5+ln⁡(1+e1+e)\boxed{0.5 + \ln\left(\frac{1+\sqrt{e}}{1+e}\right)}.

Explanation of the solution:

  1. Find the indefinite integral of 11+ex\frac{1}{1+e^x}. This is done by multiplying the numerator and denominator by e−xe^{-x} and then substituting u=e−x+1u = e^{-x}+1, or by substituting t=ext=e^x and using partial fractions. Both methods yield x−ln⁡(1+ex)x - \ln(1+e^x).
  2. Apply the limits of integration using the Fundamental Theorem of Calculus: ∫abf(x)dx=F(b)−F(a)\int_{a}^{b} f(x) dx = F(b) - F(a), where F(x)F(x) is the antiderivative of f(x)f(x).
  3. Substitute the upper limit (x=1x=1) and the lower limit (x=0.5x=0.5) into the antiderivative and subtract the results.
  4. Simplify the expression using logarithm properties.