Question

$\text{Ex:}$ $f(x)=\frac{\sin6x+\sin12x}{\cos6x+\cos12x}$

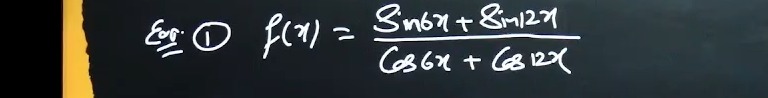
Answer 1

$\tan(9x)$

Answer 2

Using the sum-to-product trigonometric identities: $\sin A + \sin B = 2 \sin\left(\frac{A+B}{2}\right) \cos\left(\frac{A-B}{2}\right)$ $\cos A + \cos B = 2 \cos\left(\frac{A+B}{2}\right) \cos\left(\frac{A-B}{2}\right)$

For the given expression $f(x)=\frac{\sin6x+\sin12x}{\cos6x+\cos12x}$: Let $A = 12x$ and $B = 6x$. Then $\frac{A+B}{2} = \frac{12x+6x}{2} = 9x$ and $\frac{A-B}{2} = \frac{12x-6x}{2} = 3x$.

Applying the identities: Numerator: $\sin 12x + \sin 6x = 2 \sin(9x) \cos(3x)$ Denominator: $\cos 12x + \cos 6x = 2 \cos(9x) \cos(3x)$

Substituting these back into $f(x)$: $f(x) = \frac{2 \sin(9x) \cos(3x)}{2 \cos(9x) \cos(3x)}$ Assuming the denominator is non-zero (i.e., $\cos(3x) \neq 0$ and $\cos(9x) \neq 0$), we can cancel common terms: $f(x) = \frac{\sin(9x)}{\cos(9x)} = \tan(9x)$ The condition $\cos(3x) \neq 0$ ensures that the original expression is defined.