Question

${\text{ABCD}}$ is a rhombus and ${\text{P}}$, ${\text{Q}}$, ${\text{R}}$and ${\text{S}}$ are the midpoints of sides ${\text{AB}}$, ${\text{BC}}$, ${\text{CD}}$ and ${\text{DA}}$ respectively. Show that quadrilateral ${\text{PQRS}}$ is a rectangle.

Answer 1

Here we will use the property of parallelogram and rectangle which states that if opposite sides of a quadrilateral are parallel and equal then it is a parallelogram and if opposite sides of a quadrilateral are parallel and equal with all angles ${\text{9}}{{\text{0}}^0}$ then it will be a rectangle.

Step-By-Step answer:
Step 1: First of all, by drawing a diagram as per the given information in the question we get:

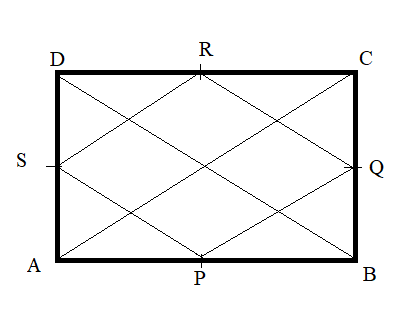
${\text{ABCD}}$ is a rhombus and
${\text{P}}$, ${\text{Q}}$, ${\text{R}}$and ${\text{S}}$ are the midpoints of sides ${\text{AB}}$, ${\text{BC}}$, ${\text{CD}}$ and ${\text{DA}}$. ${\text{BD}}$ and ${\text{AC}}$ are the respective diagonals.
Step 2: Now, as we know that, any line joining by two mid-points will be parallel to its opposite side as shown below:
${\text{RQ}}$is formed by joining the midpoints ${\text{R}}$and ${\text{Q}}$ , so we can say that ${\text{RQ}}\parallel {\text{BD}}$ and ${\text{RQ = }}\dfrac{1}{2}{\text{BD}}$……………… (1)
Similarly, ${\text{PS}}$is formed by joining the midpoints ${\text{P}}$and ${\text{S}}$ , so we can say that ${\text{PS}}\parallel {\text{BD}}$ and ${\text{PS = }}\dfrac{1}{2}{\text{BD}}$……………… (2)
By comparing the equation (1) and (2), we get:

$\Rightarrow {\text{RQ = PS}}$ also ${\text{RQ}}\parallel {\text{PS}}$
Similarly, we can prove it for the lines ${\text{RS}}$ and ${\text{PQ}}$. So, we will get ${\text{RS = PQ}}$ also ${\text{RS}}\parallel {\text{PQ}}$
Now, because ${\text{PQRS}}$, the opposite sides are equal and parallel then we can say that it is a parallelogram.
Step 3: Now for proving ${\text{PQRS}}$ is a rectangle, we need to prove that it's one angle is a right angle.
We know that
${\text{ABCD}}$ is a rhombus whose all sides are equal, so we can write as below:
${\text{AB = BC}}$
By taking half on both the side of the above expression we get:
$\Rightarrow \dfrac{1}{2}{\text{AB = }}\dfrac{1}{2}{\text{BC}}$
By substituting the value of
$\dfrac{1}{2}{\text{AB = PB}}$ and$\dfrac{1}{2}{\text{BC = BQ}}$ in the above expression we get:
$\Rightarrow {\text{PB = BQ}}$
Now, in a triangle
${\text{BPQ}}$, ${\text{PB = BQ}}$, so their opposite angles will also be equal as shown below:
$\Rightarrow \angle {\text{QPB = }}\angle {\text{PQB}}$ …………………………. (3)
Now in $\Delta {\text{APS}}$ and $\Delta {\text{CQR}}$, we can write the expressions as below:
$\Rightarrow {\text{AB = BC}}$ (sides of a rhombus are equal)
Taking half on both the sides of the above expression we get:
$\Rightarrow \dfrac{1}{2}{\text{AB = }}\dfrac{1}{2}{\text{BC}}$
By substituting the value of
$\dfrac{1}{2}{\text{AB = AP}}$ and$\dfrac{1}{2}{\text{BC = CQ}}$ in the above expression we get:

$\Rightarrow {\text{AP = CQ}}$
Similarly, we can write ${\text{AS = CR}}$ because $\dfrac{1}{2}{\text{AD = }}\dfrac{1}{2}{\text{CD}}$.
Also, we have
${\text{RQ = PS}}$, because the opposite sides of a parallelogram are equal.
So, by using SSS (side-side-side) congruence property, we can say that:
$\Rightarrow \Delta {\text{APS}} \cong \Delta {\text{CQR}}$
So, by using the property of a congruent triangle their corresponding angles will be equal. So we can write as below:
$\Rightarrow \angle {\text{SPA = }}\angle {\text{CQR}}$ ………………….. (4)
Step 4: Now we know that the sum of angles in any line will always equal ${180^0}$. So, for the line
${\text{AB}}$ we can write the equation as below:
$\Rightarrow \angle {\text{SPA + }}\angle {\text{SPQ}} + \angle {\text{QPB = 18}}{{\text{0}}^0}$ ……………………….. (5)
Similarly, for line ${\text{BC}}$, we can write the equation as below:
$\Rightarrow \angle {\text{PQB + }}\angle {\text{PQR}} + \angle {\text{CQR = 18}}{{\text{0}}^0}$
Now, by comparing the above equation with the equations (3) and (4), we get:
$\Rightarrow \angle {\text{QPB + }}\angle {\text{PQR}} + \angle {\text{SPA = 18}}{{\text{0}}^0}$ ……………………. (6)
By comparing the equation (5) and (6), we can write the equation as below:
$\Rightarrow \angle {\text{QPB + }}\angle {\text{PQR}} + \angle {\text{SPA = }}\angle {\text{SPA + }}\angle {\text{SPQ}} + \angle {\text{QPB}}$
BY eliminating the same terms from both sides of the above equation we get:
$\Rightarrow \angle {\text{PQR = }}\angle {\text{SPQ}}$ ………………….. (7)
Step 5: Now in a parallelogram
${\text{PQRS}}$, ${\text{PS}}\parallel {\text{QR}}$, because these are opposite sides of a parallelogram and ${\text{PQ}}$ is a transversal so, we can write the equation as below:
$\Rightarrow \angle {\text{PQR + }}\angle {\text{SPQ = 18}}{{\text{0}}^0}$ ($\because$ interior angles)
But we know that $\angle {\text{PQR = }}\angle {\text{SPQ}}$ (equation (7)), by substituting this value in the above equation we get:
$\Rightarrow \angle {\text{SPQ + }}\angle {\text{SPQ = 18}}{{\text{0}}^0}$
By adding into the LHS side of the above equation we get:
$\Rightarrow 2\angle {\text{SPQ = 18}}{{\text{0}}^0}$
Bringing $2$ into the LHS side of the above equation and dividing it we get:
$\Rightarrow \angle {\text{SPQ = 9}}{{\text{0}}^0}$
So, we can say that ${\text{PQRS}}$ is a rectangle.
Hence proved that ${\text{PQRS}}$ is a rectangle.

Note: Students should remember some basic properties of the quadrilateral. Some of them are mentioned below:

A quadrilateral having opposite sides equal with all angles as right angle then it is called a Rectangle.
A quadrilateral having all sides equal with all angles as right angle then it is called as Square.
A quadrilateral having opposite sides equal and parallel then it is called a parallelogram.