Solveeit Logo
Login

Question

Question: \[{\text{ABCD}}\] is a rectangle formed by the points, \[{\text{A}}\left( { - 1, - 1} \right),{\text...

ABCD{\text{ABCD}} is a rectangle formed by the points, A(−1,−1), B(−1,4), C(5,4){\text{A}}\left( { - 1, - 1} \right),{\text{ B}}\left( { - 1,4} \right),{\text{ C}}\left( {5,4} \right) and D(5,−1).{\text{D}}\left( {5, - 1} \right). P, Q, R, S{\text{P, Q, R, S}} are the mid-points of AB,BC,CD {\text{AB,BC,CD }} and DA{\text{DA}} respectively. Is the quadrilateral PQRS a square? A rectangle? Or a rhombus? Justify your answer.

Explanation

Solution

Since P,Q,R,S{\text{P,Q,R,S}} are the mid-points of side AB, BC, CD {\text{AB, BC, CD }} and DA{\text{DA}} of rectangle ABCD{\text{ABCD}}, the question can be solved by applying the midpoint formula through which we will get the coordinates of P,Q,R,S{\text{P,Q,R,S}} and finally we have to apply the distance formula and we will get a length of each side.

Complete step-by-step answer:

Firstly, applying midpoint formula, i.e., (x1+x22,y1+y22)\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)
Here P{\text{P}} is the midpoint of AB{\text{AB}}, where x1=−1,y1=−1{x_1} = - 1,{y_1} = - 1 and x2=−1,y2=4{x_2} = - 1,{y_2} = 4
We get, Coordinates of P=(−1−12,−1+42)=(−22,32)=(−1,32){\text{P}} = \left( {\dfrac{{ - 1 - 1}}{2}, \dfrac{{ - 1 + 4}}{2}} \right) = \left( { - \dfrac{2}{2},\dfrac{3}{2}} \right) = \left( { - 1,\dfrac{3}{2}} \right)
Here Q{\text{Q}} is the midpoint of BC{\text{BC}}, where x1=−1,y1=4{x_1} = - 1,{y_1} = 4 and x2=5,y2=4{x_2} = 5,{y_2} = 4
We get, Coordinates of Q = (−1+52,4+42)=(42,82)=(2,4){\text{Q = }}\left( {\dfrac{{ - 1 + 5}}{2}, \dfrac{{4 + 4}}{2}} \right) = \left( {\dfrac{4}{2}, \dfrac{8}{2}} \right) = \left( {2,4} \right)
Here R{\text{R}} is the midpoint of CD{\text{CD}}, where x1=5,y1=4{x_1} = 5,{y_1} = 4and x2=5,y2=−1{x_2} = 5,{y_2} = - 1
Coordinates of R=(5+52,−1+42)=(102,32)=(5,32){\text{R}} = \left( {\dfrac{{5 + 5}}{2}, \dfrac{{ - 1 + 4}}{2}} \right) = \left( {\dfrac{{10}}{2},\dfrac{3}{2}} \right) = \left( {5, \dfrac{3}{2}} \right)
Here S{\text{S}} is the midpoint of DA{\text{DA}}, where x1=5,y1=−1{x_1} = 5,{y_1} = - 1 and x2=−1,y2=−1{x_2} = - 1,{y_2} = - 1
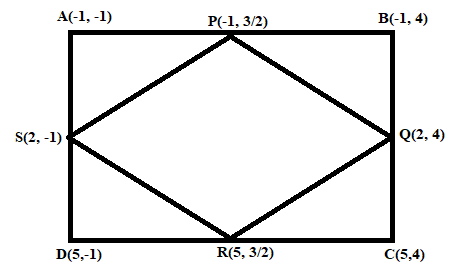
Coordinates of S=(−1+52,−1−12)=(42,−22)=(2,−1)S = \left( {\dfrac{{ - 1 + 5}}{2}, \dfrac{{ - 1 - 1}}{2}} \right) = \left( {\dfrac{4}{2}, - \dfrac{2}{2}} \right) = \left( {2, - 1} \right),
Therefore, vertices of the quadrilateral PQRS are P(−1,32)P\left( { - 1, \dfrac{3}{2}} \right), Q(2,4)Q(2,4), R(5,32)R\left( {5,\dfrac{3}{2}} \right), S(2,1)S(2,1)

Now, by applying distance formula, i.e., (x2−x1)2+(y2−y1)2\sqrt {({x_2} - {x_1})_{}^2 + ({y_2} - {y_1})_{}^2} , we can find out the length of all the sides of the quadrilateral PQRS{\text{PQRS}}
So, length of side PQ=(−1−2)2+(32−4)2=(−3)2+(−52)2=9+254=614PQ = \sqrt {( - 1 - 2)_{}^2 + \left( {\dfrac{3}{2} - 4} \right)_{}^2} = \sqrt {( - 3)_{}^2 + \left( { - \dfrac{5}{2}} \right)_{}^2} = \sqrt {9 + \dfrac{{25}}{4}} = \sqrt {\dfrac{{61}}{4}}
Here x2=−1,x1=2,y2=32,y1=4{x_2} = - 1,{x_1} = 2,{y_2} = \dfrac{3}{2},{y_1} = 4
Length of side QR=(2−5)2+(4−32)2=(−3)2+(52)2=9+254=614QR = \sqrt {(2 - 5)_{}^2 + \left( {4 - \dfrac{3}{2}} \right)_{}^2} = \sqrt {( - 3)_{}^2 + \left( {\dfrac{5}{2}} \right)_{}^2} = \sqrt {9 + \dfrac{{25}}{4}} = \sqrt {\dfrac{{61}}{4}}
Here x2=2,x1=5,y2=−3,y1=52{x_2} = 2, {x_1} = 5, {y_2} = - 3, {y_1} = \dfrac{5}{2}
Length of side RS=(5−2)2+(32+1)2=(3)2+(52)2=9+244=614RS = \sqrt {(5 - 2)_{}^2 + \left( {\dfrac{3}{2} + 1} \right)_{}^2} = \sqrt {(3)_{}^2 + \left( {\dfrac{5}{2}} \right)_{}^2} = \sqrt {9 + \dfrac{{24}}{4}} = \sqrt {\dfrac{{61}}{4}}
Here x2=5,x1=2,y2=32,y1=−1{x_2} = 5, {x_1} = 2, {y_2} = \dfrac{3}{2}, {y_1} = - 1
Length of side SP=(2+1)2+(−1−32)2=(3)2+(−52)2=9+254=614SP = \sqrt {(2 + 1)_{}^2 + \left( { - 1 - \dfrac{3}{2}} \right)_{}^2} = \sqrt {(3)_{}^2 + \left( { - \dfrac{5}{2}} \right)_{}^2} = \sqrt {9 + \dfrac{{25}}{4}} = \sqrt {\dfrac{{61}}{4}}
Here x2=2,x1=−1,y2=−1,y1=32{x_2} = 2, {x_1} = - 1, {y_2} = - 1, {y_1} = \dfrac{3}{2}
Since all the sides of the quadrilateral PQRS{\text{PQRS}} so it is clear that it can be either square or rhombus. So now we have to find out the length of the diagonal to check whether it is a square or quadrilateral.
Here, we applying distance formula (x2−x1)2+(y2−y1)2\sqrt {({x_2} - {x_1})_{}^2 + ({y_2} - {y_1})_{}^2}
We get, Length of the diagonal PR=(−1−5)2+(32−32)2=(−6)2+0=36=6PR = \sqrt {( - 1 - 5)_{}^2 + \left( {\dfrac{3}{2} - \dfrac{3}{2}} \right)_{}^2} = \sqrt {( - 6)_{}^2 + 0 = } \sqrt {36} = 6 ,
Here x2=−1,x1=5,y2=32,y1=32{x_2} = - 1, {x_1} = 5, {y_2} = \dfrac{3}{2}, {y_1} = \dfrac{3}{2}
Length of the diagonal QS=(2−2)2+(4+1)2=0+(5)2=25=5QS = \sqrt {(2 - 2)_{}^2 + (4 + 1)_{}^2} = \sqrt {0 + (5)_{}^2} = \sqrt {25} = 5
Here x2=2,x1=2,y2=4,y1=−1{x_2} = 2, {x_1} = 2, {y_2} = 4, {y_1} = - 1
Since the length of the diagonals of the quadrilateral PQRS{\text{PQRS}} are not equal but the length of the sides are equal so it is a rhombus.

Note: There are six types of quadrilateral like rhombus, square, parallelogram, rectangle, trapezium and cyclic quadrilateral.
In the case of squares, all the sides and diagonals are of equal length.
In the case of rhombus all sides are equal, and the diagonals are not equal and form right angles.