Question

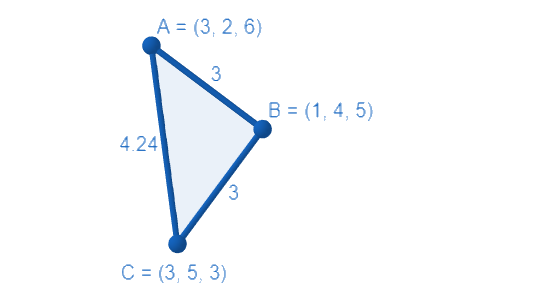
$\text{A}\left( \text{3,2}\text{.6} \right)\text{,B}\left( \text{1,4,5} \right)\text{ and C}\left( \text{3,5,3} \right)$ are the vertices of triangle ABC. Find $m\angle ABC$.
a) $\dfrac{\pi }{2}$
b) $\dfrac{\pi }{4}$
c) $\dfrac{\pi }{6}$
d) $\dfrac{\pi }{3}$

Answer 1

First find the direction ratios of BA and BC b using formula that if points are given $\left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right)$ and $\left( {{a}_{2}},{{b}_{2}},c \right)$ then the direction ratio will be $\left( \left( {{a}_{2}}-{{a}_{1}} \right),\left( {{b}_{2}}-{{b}_{1}} \right),\left( {{c}_{2}}-{{c}_{1}} \right) \right)$ then find the angle using the formula $\cos \theta =\dfrac{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}\sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}$
If $\theta$ is angle contained between line segment of ratios $\left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right)$ and $\left( {{a}_{2}},{{b}_{2}},{{c}_{2}} \right)$

Complete step-by-step answer:
In the question the vertices of the triangle are given such as A(3, 2, 6), B(1, 4, 5) and c(3, 5, 3) we have found the angle of ABC.
So,now to find the angle of ABC we have to find the direction ratios of the line segment joining BA and BC using formula there are two points let's suppose X(x, y, z) $Y\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ then the direction ratios of XY will be $\left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}} \right)$ .
Now by using the formula we will use the A point is (3, 2, 6) and B point is (1, 4, 5).
So the direction ratios of BA by using the formula so we get direction ratios as,
BA = (3 – 1, 2 – 4, 6 – 5) which is equal to (2, -2,1)
Now by using the formula we will use the points BC(1, 4, 5) and (3, 5, 3). So the direction ratios of BC by using the formula we get direction ratios as,
BC = (3 – 1, 5 – 4, 3 – 5) which is equal to (2, 1, -2)
If the direction ratios are known such as $\left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right)$and $\left( {{a}_{2}},{{b}_{2}},{{c}_{2}} \right)$and the angle contained in them is $\theta$ then, we can apply formula,
$\cos \theta =\dfrac{{{a}_{1}}{{a}_{2}},+{{b}_{1}}b+{{c}_{1}}{{c}_{2}}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}\times \sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}$
So by substituting the direction ratios as (2, -2, 1) and (2, 1, -2)
So $\cos \theta =\dfrac{2\times 2+\left( -2 \right)\times 1+1\left( -2 \right)}{\sqrt{{{2}^{2}}+{{\left( -2 \right)}^{2}}+1}\sqrt{{{2}^{2}}+{{1}^{2}}+{{\left( -2 \right)}^{2}}}}$
So by doing we get,
$\cos \theta =\dfrac{4-2-2}{3\times 3}=0$
If $\cos \theta =0$
Then $\theta ={{90}^{\circ }}$
So the angle at B will be ${{90}^{\circ }}$

So, the correct answer is “Option A”.

Note: Here, we can also use the following method; we will first find the distance between all the points to find the length of the sides that is AB, BC and CA. So, we will use the distance formula for $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ , that is: $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$ , therefore:
AB $=\sqrt{{{\left( 1-3 \right)}^{2}}+{{\left( 4-2 \right)}^{2}}+{{\left( 5-6 \right)}^{2}}}=3$ , BC $=\sqrt{{{\left( 3-1 \right)}^{2}}+{{\left( 5-4 \right)}^{2}}+{{\left( 3-5 \right)}^{2}}}=2$ ,
CA $=\sqrt{{{\left( 3-3 \right)}^{2}}+{{\left( 5-2 \right)}^{2}}+{{\left( 3-6 \right)}^{2}}}=4.24$
Now, we will see if the Pythagoras theorem holds for this triangle, for this $C{{A}^{2}}=A{{B}^{2}}+B{{C}^{2}}$ , after putting the value we will get: ${{\left( 4.24 \right)}^{2}}={{3}^{2}}+{{3}^{2}}\Rightarrow 18=8$ , therefore the given triangle is right angled at B. Hence $m\angle ABC=\dfrac{\pi }{2}$ .