Solveeit Logo
Login

Question

Question: Tension in the rope at the rigid support is: (Take \(g = 10\;ms^{-2}\)) ![](https://www.vedantu.co...

Tension in the rope at the rigid support is: (Take g=10  ms−2g = 10\;ms^{-2})

A). 760 N
B). 41360 N
C). 1580 N
D). 1620 N

Explanation

Solution

Use free-body diagrams on each climber to determine the tension that is imparted by each climber to the rope due to their weight as well as their acceleration, if any. In the case of climber B, recall that constant velocity of descent implies no acceleration. To this end, determine the net tension acting on the rope at the rigid support by taking the sum of tensions imparted by each climber.

Formula Used:
Fgravity=mgF_{gravity} = mg
Facceleration=maF_{acceleration} = ma

Complete step-by-step solution:
The tension in the rope at the rigid support will be the additive sum of tension imparted to the rope by each climber. The forces acting on the climber and the tension imparted to the rope is as shown in the figure. Let us look at each climber individually.
For climber A ascending upwards:
mA=60  kgm_A = 60\;kg and aA=2  ms−2a_A = 2\;ms^{-2}
From the figure, we see that,
T1–mAg=mAaA⇒T1=mAg+mAaAT_1 – m_Ag = m_Aa_A \Rightarrow T_1 = m_Ag + m_Aa_A
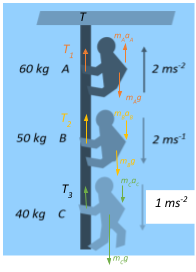
⇒T=(60×10)+(60×2)=600+120=720  N\Rightarrow T = (60 \times 10) + (60 \times 2) = 600 + 120 = 720\;N

For climber B descending downwards:
mB=50  kgm_B =50\;kg and constant velocity v=2  ms−1v = 2\;ms^{-1} which means that acceleration aB=0a_B = 0
From the figure, we see that,
T2−mBg=0⇒T2=mBg=50×10=500  NT_2-m_Bg = 0 \Rightarrow T_2 = m_B g = 50 \times 10 = 500\;N
For climber C descending downwards:
mC=40  kgm_C = 40\;kg and aC=1  ms−2a_C = 1\;ms^{-2}
From the figure we see that,
T3=mCg−mCaC=(40×10)−(40×1)=400−40=360  NT_3 = m_Cg-m_Ca_C = (40 \times 10)-(40 \times 1) = 400-40 = 360\;N
Therefore, the net tension at the rigid support would be:
T=T1+T2+T3=720+500+360=1580  NT = T_1 +T_2 +T_3 = 720 + 500 + 360 = 1580\;N
Therefore, the correct option would be C. 1580 N

Note: Always use free body diagrams to summarize the list of all influencing forces in a system as this ensures that all forces are accounted for. This also guarantees that we are directionally-conscious while deducing the forces and their contribution, since the net force will always depend on the direction in which individual forces act.
Also, do not mistake downward acceleration for deceleration since this implies that there is an acceleration but in the downward direction, whereas deceleration implies a diminishing rate of velocity. The effect of downward acceleration is accounted for by the force that defines it, so there is no need to use a negative sign to signify acceleration in the downward direction. Negative sign for acceleration is thus always reserved to indicate deceleration.