Question
Question: $\tan\left(\tan^{-1}(-1)+\frac{\pi}{3}\right)$...
tan(tan−1(−1)+3π)
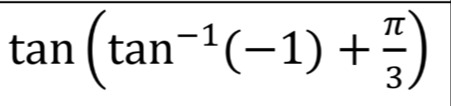
Answer
2 - 3
Explanation
Solution
Evaluate tan−1(−1) to find −4π. Substitute this into the expression to get tan(−4π+3π). Apply the tangent addition formula tan(A+B)=1−tanAtanBtanA+tanB with tan(−4π)=−1 and tan(3π)=3. This yields 1−(−1)3−1+3=1+33−1. Rationalizing the denominator gives the final answer 2−3.
