Question

Tangents drawn from the point P(1, 8) to the circle touch ${{x}^{2}}+{{y}^{2}}-6x-4y-11=0$ the circle at the points A and B. The equation of the circumcircle of the triangle PAB is
(a) ${{x}^{2}}+{{y}^{2}}+4x-6y+19=0$
(b) ${{x}^{2}}+{{y}^{2}}-4x-10y+19=0$
(c) ${{x}^{2}}+{{y}^{2}}-2x+6y-29=0$
(d) ${{x}^{2}}+{{y}^{2}}-6x-4y+19=0$

Answer 1

Hint: We will first draw the figure from all the mentioned details in the question. And then from the given equation of the circle we will find the center of the circle by comparing it with the general form of the circle. Also we will make use of the fact that the diameter of the circle subtends a right angle at any point on the circumference.

Complete step-by-step answer:
Drawing the figure from the given details.

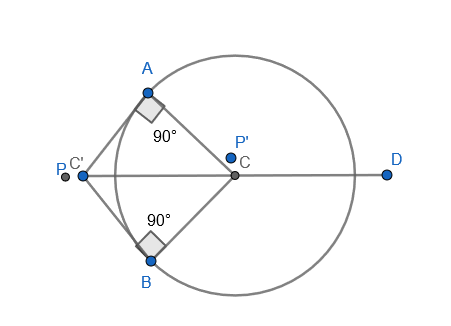
We know that the general form of circle is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$. In this the centre of the circle is represented by (-g, -f). So comparing ${{x}^{2}}+{{y}^{2}}-6x-4y-11=0$ this with the general form of circle we get the coordinates of the center as (3,2) as 2g is equal to -6 and 2f is equal to -4.
Now we know that the diameter of the circle subtends a right angle at any point on the circumference. Hence the circumference of triangle PAB is a circle on PC as diameter whose equation is,
$\Rightarrow (x-1)(x-3)+(y-8)(y-2)........(1)$
Now first multiplying the x terms together and the y terms together by opening the brackets in equation (1) and hence we get,
$\Rightarrow x(x-3)-1(x-3)+y(y-2)-8(y-2)........(2)$
Now again multiplying all the terms and rearranging in equation (2) we get,
$\Rightarrow {{x}^{2}}-3x-x+3+{{y}^{2}}-2y-8y+16........(3)$
Now adding like terms together and rearranging in equation (3) we get,
$\Rightarrow {{x}^{2}}+{{y}^{2}}-4x-10y+19=0$
Hence the correct answer is option (b).

Note: Drawing the figures in these types of questions is very important because then things gets clearer. We in a hurry can make mistakes in calculating the center of the circle by writing (-3,-2) instead of (3,2) and hence we need to be careful while doing this step.