Solveeit Logo
Login

Question

Question: Tangents are drawn to the circle \({x^2} + {y^2} = 12\) at the points where it is met by the circle ...

Tangents are drawn to the circle x2+y2=12{x^2} + {y^2} = 12 at the points where it is met by the circle x2+y2−5x+3y−2=0;{x^2} + {y^2} - 5x + 3y - 2 = 0; Find the point of intersection of these tangents.

Explanation

Solution

Hint: Two circles are given. They will intersect at two points. We will draw the tangents from those two points. We have to find the point of intersection of those two tangents. The two intersection points form a common chord to both the circle.

Complete step-by-step answer:
The graphical representation of the given problem is similar to the below figure.

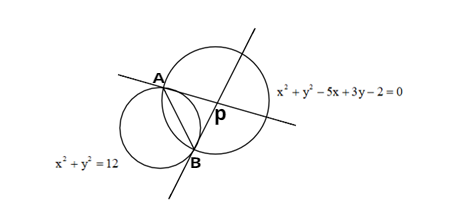
The given circles are x2+y2=12{x^2} + {y^2} = 12 and x2+y2−5x+3y−2=0{x^2} + {y^2} - 5x + 3y - 2 = 0. These two circles intersect at two points. Let those points be A and B.
x2+y2−12=0{x^2} + {y^2} - 12 = 0 ... (1)
x2+y2−5x+3y−2=0{x^2} + {y^2} - 5x + 3y - 2 = 0 ... (2)
Let the tangents passing through A and B meet at point P (h, k).
We need to find the coordinates of point P, i.e., h, k values.
The points A, B form a chord to both the circles. The line AB is the common chord to both the circles.
Equation of common chord to the given circles will be equation (1) – equation (2),
⇒(x2+y2−12)−(x2+y2−5x+3y−2)=0\Rightarrow ({x^2} + {y^2} - 12) - ({x^2} + {y^2} - 5x + 3y - 2) = 0
On simplification, we get
⇒−12+5x−3y+2=0\Rightarrow - 12 + 5x - 3y + 2 = 0
⇒5x−3y−10=0\Rightarrow 5x - 3y - 10 = 0 ... (3)
Therefore, the equation of the chord AB is 5x−3y−10=05x - 3y - 10 = 0
Since AB is the point of contact with respect to P (h, k) for the circle x2+y2−12=0{x^2} + {y^2} - 12 = 0.
⇒\RightarrowEquation of the AB is xh+yk−12=0xh + yk - 12 = 0 ... (4)
Comparing equation (3) and equation (4), we get
\eqalign{ & \Rightarrow \dfrac{h}{5} = - \dfrac{k}{3} = \dfrac{{12}}{{10}} \cr & \Rightarrow \dfrac{h}{5} = - \dfrac{k}{3} = \dfrac{6}{5} \cr}
⇒h=6,k=−185\Rightarrow h = 6,k = \dfrac{{ - 18}}{5}
∴\therefore The point of intersection of two tangents is P(h, k) = (6,−185)\left( {6,\dfrac{{ - 18}}{5}} \right)
Note: If the tangents drawn to the circle x2+y2−a2=0{x^2} + {y^2} - {a^2} = 0 at A and B meet at point P (h, k) , then AB will be the chord of contact of the tangents to that circle from P. Therefore the equation of AB will be hx+ky−a2=0hx + ky - {a^2} = 0. We compared equations (3), (4) because those two equations represent the same line. If two equations are representing the same line, then their coefficients must be proportional.