Question

Tangents are drawn to a parabola from a point T. If P, Q are the points of contact then the perpendicular distance from P, T, and Q upon the tangent at the vertex of the parabola are in
(A). A.P
(B). G.P
(C). H.P
(D). None of the above

Answer 1

Hint: To solve the question, we have to apply the standard parabola equations and formula for calculating the points P, Q. Then, apply the formula for the tangent of the parabola at points P and Q and solve the obtained equations to calculate the value of point T. We have to apply the concept that the perpendicular distance from the point of contact to the vertex is equal to x-coordinate of the given point of contact. Thus, we can analyze the obtained distances to arrive at the right choice.

Complete step-by-step solution -
Given
Let the points P, Q on parabola ${{y}^{2}}=4ax$ be $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right),\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$ respectively.
We know that the general form of tangent to the parabola is given by $ty=x+a{{t}^{2}}$ at point $\left( a{{t}^{2}},2at \right)$.
The figure can be as shown below,

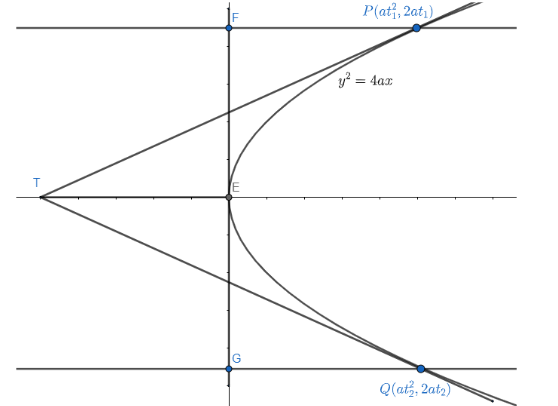
Thus, by substituting the values of points in the above equation we get
The tangent to the parabola from point P is ${{t}_{1}}y=x+a{{t}_{1}}^{2}$.
The tangent to the parabola from point Q is ${{t}_{2}}y=x+a{{t}_{2}}^{2}$.
We know that the point of intersection of tangents at P, Q is point T.
Thus, by subtracting the above tangent equations, we get

& {{t}_{1}}y-{{t}_{2}}y=x+a{{t}_{1}}^{2}-\left( x+a{{t}_{2}}^{2} \right) \\\ & {{t}_{1}}y-{{t}_{2}}y=x+a{{t}_{1}}^{2}-x-a{{t}_{2}}^{2} \\\ & y\left( {{t}_{1}}-{{t}_{2}} \right)=a\left( {{t}_{1}}^{2}-{{t}_{2}}^{2} \right) \\\ \end{aligned}$$ We know the formula $${{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)$$ Thus, by applying the formula, we get $$\begin{aligned} & y\left( {{t}_{1}}-{{t}_{2}} \right)=a\left( {{t}_{1}}-{{t}_{2}} \right)\left( {{t}_{1}}+{{t}_{2}} \right) \\\ & y=\dfrac{a\left( {{t}_{1}}-{{t}_{2}} \right)\left( {{t}_{1}}+{{t}_{2}} \right)}{\left( {{t}_{1}}-{{t}_{2}} \right)} \\\ & y=a\left( {{t}_{1}}+{{t}_{2}} \right) \\\ \end{aligned}$$ By substituting the y value in tangent equation at point P, we get $$\begin{aligned} & {{t}_{1}}a\left( {{t}_{1}}+{{t}_{2}} \right)=x+a{{t}_{1}}^{2} \\\ & a{{t}_{1}}^{2}+a{{t}_{1}}{{t}_{2}}=x+a{{t}_{1}}^{2} \\\ & \Rightarrow x=a{{t}_{1}}^{2}+a{{t}_{1}}{{t}_{2}}-a{{t}_{1}}^{2} \\\ & x=a{{t}_{1}}{{t}_{2}} \\\ \end{aligned}$$ Thus, we get the point T is $$\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$$.  From the above figure, we have FG is the tangent through the vertex of the parabola. So, the perpendicular distance from P, T, and Q upon the tangent at the vertex of the parabola are PF, TE, and QG respectively. So, from the above figure, it is clear that the perpendicular distance is equal to x-coordinate of P, T, and Q respectively. Thus, we get The perpendicular distance from P, T and Q upon the tangent at the vertex of the parabola are $$a{{t}_{1}}^{2},a{{t}_{1}}{{t}_{2}},a{{t}_{2}}^{2}$$ respectively. Now we will check what series is this. By observing we see that, $$\dfrac{a{{t}_{1}}{{t}_{2}}}{a{{t}_{1}}^{2}}=\dfrac{{{t}_{2}}}{{{t}_{1}}},\dfrac{a{{t}_{2}}^{2}}{a{{t}_{1}}{{t}_{2}}} =\dfrac{{{t}_{2}}}{{{t}_{1}}}$$ We know that the series of numbers with common ratio are termed as terms of Geometric progression. Thus, the perpendicular distance from P, T, and Q upon the tangent at the vertex of the parabola are in G.P. Hence, option (b) is the right choice. Note: The possibility of mistake can be, not using standard parabola equations and formula for calculating the points P, Q. The alternative way of solving is applying direct formula which states that the points of intersection of the tangents at the points $$\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right),\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$$ is $$\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)$$. Thus, we can arrive at the right choice.