Solveeit Logo
Login

Question

Question: Tangent to the ellipse \(\dfrac{{{x^2}}}{{32}} + \dfrac{{{y^2}}}{{18}} = 1\) having slope \[\dfrac{{...

Tangent to the ellipse x232+y218=1\dfrac{{{x^2}}}{{32}} + \dfrac{{{y^2}}}{{18}} = 1 having slope −34\dfrac{{ - 3}}{4} meet the coordinate axis at A and B. Then, the area of △AOB\vartriangle AOB, where O is the origin is
A. 12 sq. units.
B. 8 sq. units.
C. 24 sq. units.
D. 32 sq. units.

Explanation

Solution

To solve this question, we will use the general equation of tangent to ellipse in slope form, which is given by y=mx±a2m2+b2y = mx \pm \sqrt {{a^2}{m^2} + {b^2}} where m is the slope of tangent and a and b are the x and y intercepts respectively.

Complete step-by-step answer:

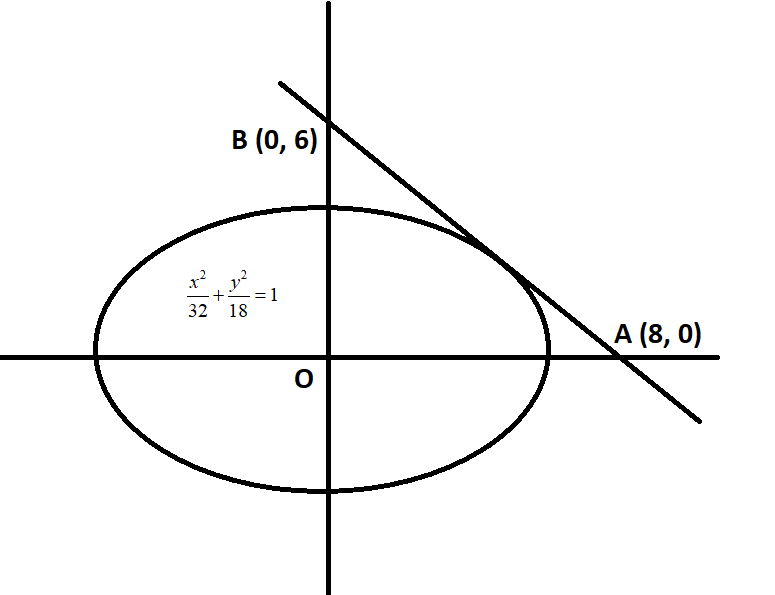
Given that,
Equation of ellipse = x232+y218=1\dfrac{{{x^2}}}{{32}} + \dfrac{{{y^2}}}{{18}} = 1 ….. (i)
Comparing this with the general equation of ellipse x2a2+y2b2=1\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1
We get a=32,b=18a = \sqrt {32} ,b = \sqrt {18}
Slope of tangent, m = −34\dfrac{{ - 3}}{4}
We know that,
The equation of tangent to ellipse in slope form is given by
⇒y=mx±a2m2+b2\Rightarrow y = mx \pm \sqrt {{a^2}{m^2} + {b^2}}
Putting the values of a, b and m, we will get
⇒y=−34x±32×(−34)2+18\Rightarrow y = \dfrac{{ - 3}}{4}x \pm \sqrt {32 \times {{\left( {\dfrac{{ - 3}}{4}} \right)}^2} + 18}
⇒y=−34x±32×916+18\Rightarrow y = \dfrac{{ - 3}}{4}x \pm \sqrt {32 \times \dfrac{9}{{16}} + 18}
⇒y=−34x±2×9+18\Rightarrow y = \dfrac{{ - 3}}{4}x \pm \sqrt {2 \times 9 + 18}
⇒y=−34x±36\Rightarrow y = \dfrac{{ - 3}}{4}x \pm \sqrt {36}
⇒y=−34x±6\Rightarrow y = \dfrac{{ - 3}}{4}x \pm 6
Simplifying this, we will get
⇒4y=−3x±24\Rightarrow 4y = - 3x \pm 24
⇒4y+3x=±24\Rightarrow 4y + 3x = \pm 24
We get,
⇒4y+3x=24\Rightarrow 4y + 3x = 24
And,
⇒4y+3x=−24\Rightarrow 4y + 3x = - 24
Both equations are tangent to the ellipse.
According to the question, the tangents meet the coordinate axis at A and B.
So, we will put y = 0 in the above equations.
⇒4(0)+3x=24\Rightarrow 4\left( 0 \right) + 3x = 24
⇒x=8\Rightarrow x = 8
And,
⇒4(0)+3x=−24\Rightarrow 4\left( 0 \right) + 3x = - 24
⇒x=−8\Rightarrow x = - 8
So, the point A is (8,0)\left( {8,0} \right) or (−8,0)\left( { - 8,0} \right)
Now, put x = 0 in the above equations,
We will get,
⇒y=6 or −6\Rightarrow y = 6{\text{ or }} - 6
So, the point B is (0,6)\left( {0,6} \right) or (0,−6)\left( {0, - 6} \right)
⇒△AOB\Rightarrow \vartriangle AOB is a right-angled triangle, where O is the origin.
We know that,
Area of triangle = 12×base×height\dfrac{1}{2} \times base \times height
So, the area of △AOB\vartriangle AOB = 12×∣OA∣×∣OB∣\dfrac{1}{2} \times \left| {OA} \right| \times \left| {OB} \right|
We have ∣OA∣\left| {OA} \right| = 8 and ∣OB∣\left| {OB} \right| = 6
the area of △AOB\vartriangle AOB = 12×8×6=24sq.units\dfrac{1}{2} \times 8 \times 6 = 24sq.units

So, the correct answer is “Option C”.

Note: Whenever we ask such types of questions, the key concept to solve these questions is the general equation of tangent to ellipse in slope form. Using that equation and putting the appropriate given values, we will get the required answer.