Question
Question: Tangent \(\overleftrightarrow {PC}\) intersects the circle \(O\) at \(C\) , chord \(\overline {AB} |...
Tangent PC intersects the circle O at C , chord AB∣∣CP , diameter COD intersects AB at E , and diameter AOF is extended to P . If ∠OAE=30∘ , find mF\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{B} and mB\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{D} .
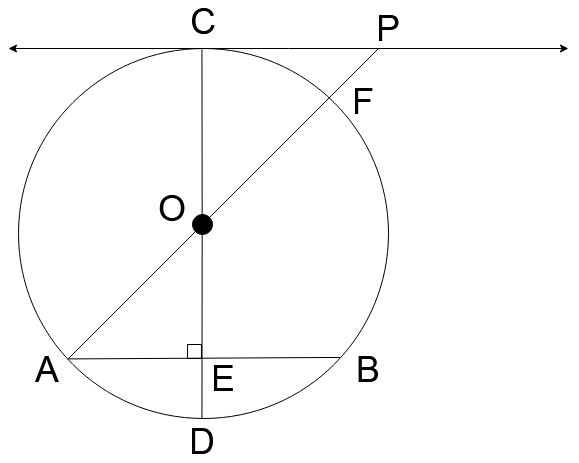
Solution
You can start by explaining why we need to calculate the angles corresponding to the given arcs and write the equation for finding the length of the arc, i.e. Length of an arc =2πr360n . Then calculate the angle ∠AOE by using the property of the triangle that states that the sum of all the angles in a triangle is 180∘ . Then use the concept of vertically opposite angles to find ∠COF . Then calculate the values of ∠FOB and ∠BOD . Then put these values in the equation Length of an arc =2πr360n to reach the solution.
Complete step by step answer:
Let’s start the solution by redrawing the above diagram in the following manner -
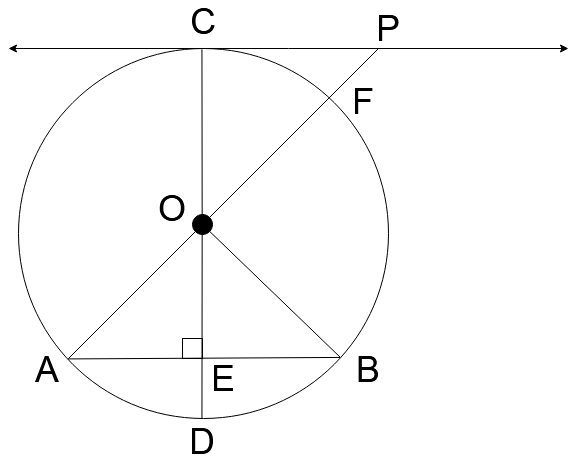
Now, in this problem, we have to find mF\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{B} and mB\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{D} . Both of these are arcs and we know for a fact that the length of an arc can be calculated by using the angle which the two ends points of the arc make at the center. For this, we use the following equation
Length of an arc =2πr360n (Equation 1)
Here, n= the angle that the two endpoints of the arc make at the center
So in this case to calculate mF\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{B} we have to calculate ∠FOB and to find out mB\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{D} , we have to calculate the value of ∠BOD .
To solve this question we will first use a very interesting property of triangles. A triangle has 3 angles and the sum of all the three angles is always equal to 180∘ .
So, we now know that in ΔAOE
∠AOE+∠OEA+∠OAE=180∘
Given in the problem,
∠OAE=30∘
∠OEA=90∘ (Chords are always perpendicular to the radius)
So, ∠AOE+90∘+30∘=180∘
∠AOE=60∘
We can also say that
∠AOE=∠COF=60∘ (Vertically opposite angles)
Now,
∵∠AEO=∠OEB=90∘
∵OE=OE (Common)
∵OA=OB= Radius
∴ΔAOE≅ΔOBE
∴∠AOE=∠EOB=60∘
We, also know
∠AOE+∠FOB+∠EOB=180∘ (They all lie on a straight line)
∴∠FOB=60∘
So using equation 1 to calculate the value of mF\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{B} , we get
mFB\lower0.5em⌢=2πr36060
mFB\lower0.5em⌢=31πr
Also, ∠EOB=∠BOD=60∘
So using equation 1 to calculate the value of mB\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{D} , we get
mBD\lower0.5em⌢=2πr36060
mBD\lower0.5em⌢=31πr
Hence, mF\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{B} and mB\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{D} are both equal to 31πr .
Note: In such a type of problem we can easily solve by using the basic properties of arcs in a circle. But, it is especially very important to remember what symbols represent what part. For example, we are given PC that represents a tangent, COD that represents a diameter, AB represents a chord, and mF\overset{\lower0.5em\hbox{\smash{\scriptscriptstyle\frown}}}{B} represents an arc.
