Question

$\tan^4x + \tan^4y + 2cot^2x \cdot cot^2y = 3 + \sin^2(x+y)$

$(x+y)_{min} = ?$

$x,y>0$

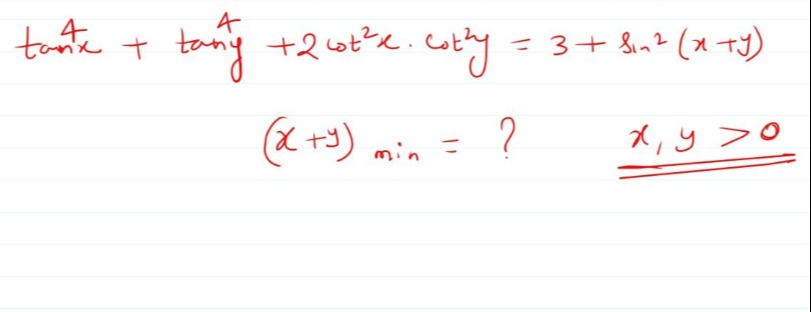
Answer 1

$\frac{\pi}{2}$

Answer 2

The problem involves an equation with trigonometric functions. The strategy is to analyze the range of values for both the Left Hand Side (LHS) and the Right Hand Side (RHS) of the equation.

1. Analyze LHS: Use the AM-GM inequality, $\frac{a+b}{2} \ge \sqrt{ab}$, repeatedly.

   • First, apply AM-GM to $\tan^4x$ and $\tan^4y$ to get $\tan^4x + \tan^4y \ge 2\tan^2x \tan^2y$.
   • Substitute this into the LHS, which becomes $2\tan^2x \tan^2y + 2\cot^2x \cot^2y$.
   • Let $P = \tan^2x \tan^2y$. The expression becomes $2P + \frac{2}{P}$.
   • Apply AM-GM again to $2P$ and $\frac{2}{P}$ to get $2P + \frac{2}{P} \ge 4$.
   • Thus, LHS $\ge 4$. The equality holds when $\tan^2x = \tan^2y = 1$.

2. Analyze RHS: Use the known range of $\sin^2\theta$.

   • $0 \le \sin^2(x+y) \le 1$.
   • Adding 3, we get $3 \le 3 + \sin^2(x+y) \le 4$.
   • Thus, RHS $\le 4$.

3. Equate LHS and RHS: For the given equation to hold, since LHS $\ge 4$ and RHS $\le 4$, both sides must be equal to 4.

   • LHS = 4 implies $\tan^2x = 1$ and $\tan^2y = 1$.
   • RHS = 4 implies $\sin^2(x+y) = 1$.

4. Find minimal (x+y):

   • From $\tan^2x = 1$ and $x>0$, possible values for $x$ are $\frac{\pi}{4}, \frac{3\pi}{4}, \frac{5\pi}{4}, \dots$. Similarly for $y$.
   • From $\sin^2(x+y) = 1$, possible values for $x+y$ are $k\pi + \frac{\pi}{2}$ for integer $k$.
   • Test combinations of the smallest $x,y$ values that satisfy $\tan^2x=1$ and $\tan^2y=1$.
   • The smallest $x,y$ are $x=\frac{\pi}{4}$ and $y=\frac{\pi}{4}$. Their sum is $x+y=\frac{\pi}{2}$.
   • Check if $\sin^2(\frac{\pi}{2})=1$. Yes, it is.
   • This gives the minimum possible value for $x+y$. Other combinations like $x=\frac{\pi}{4}, y=\frac{3\pi}{4}$ give $x+y=\pi$, but $\sin^2(\pi)=0 \ne 1$, so these are not solutions.

The minimum value of $(x+y)$ is $\frac{\pi}{2}$.