Question
Question: $\tan^{-1}x, x < 0$ is equal to...
tan−1x,x<0 is equal to
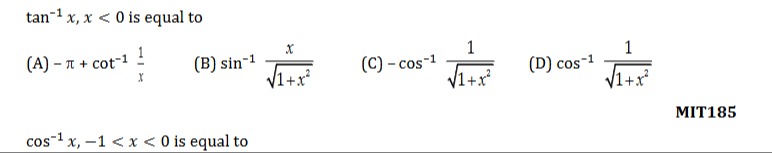
−π+cot−1x1
sin−11+x2x
−cos−11+x21
cos−11+x21
(A), (B), (C)
Solution
Let y=tan−1x. For x<0, the range of y is (−2π,0).
Option (A): For x<0, x1<0. The principal value of cot−1z for z<0 lies in (2π,π). Thus, for x<0, cot−1x1∈(2π,π). Consequently, −π+cot−1x1∈(−π+2π,−π+π)=(−2π,0). This range matches the range of tan−1x for x<0. The identity tan−1x=−π+cot−1x1 holds for x<0.
Option (B): We know that for y=tan−1x, where −2π<y<2π, siny=1+tan2ytany=1+x2x. Since y∈(−2π,2π), y=sin−1(1+x2x). This identity holds for all real x. For x<0, 1+x2x∈(−1,0), so sin−11+x2x∈(−2π,0), matching the range of tan−1x.
Option (C): For y=tan−1x, cosy=1+tan2y1=1+x21 for y∈(−2π,2π). Since x<0, y∈(−2π,0). Let z=−y. Then z∈(0,2π). cosz=cos(−y)=cosy=1+x21. Since z∈(0,2π), z=cos−1(1+x21). Substituting z=−y, we get −y=cos−1(1+x21), which means y=−cos−1(1+x21). This identity holds for x≤0. For x<0, 1+x21∈(0,1), so cos−11+x21∈(0,2π). Thus, −cos−11+x21∈(−2π,0), matching the range of tan−1x.
Option (D): For x<0, cos−11+x21∈(0,2π), which does not match the range of tan−1x for x<0, which is (−2π,0). Thus, option (D) is incorrect.
