Question
Question: $\tan^{-1}\tan x$ where $x \in [\frac{2027\pi}{2},\frac{2029\pi}{2}]$...
tan−1tanx where x∈[22027π,22029π]
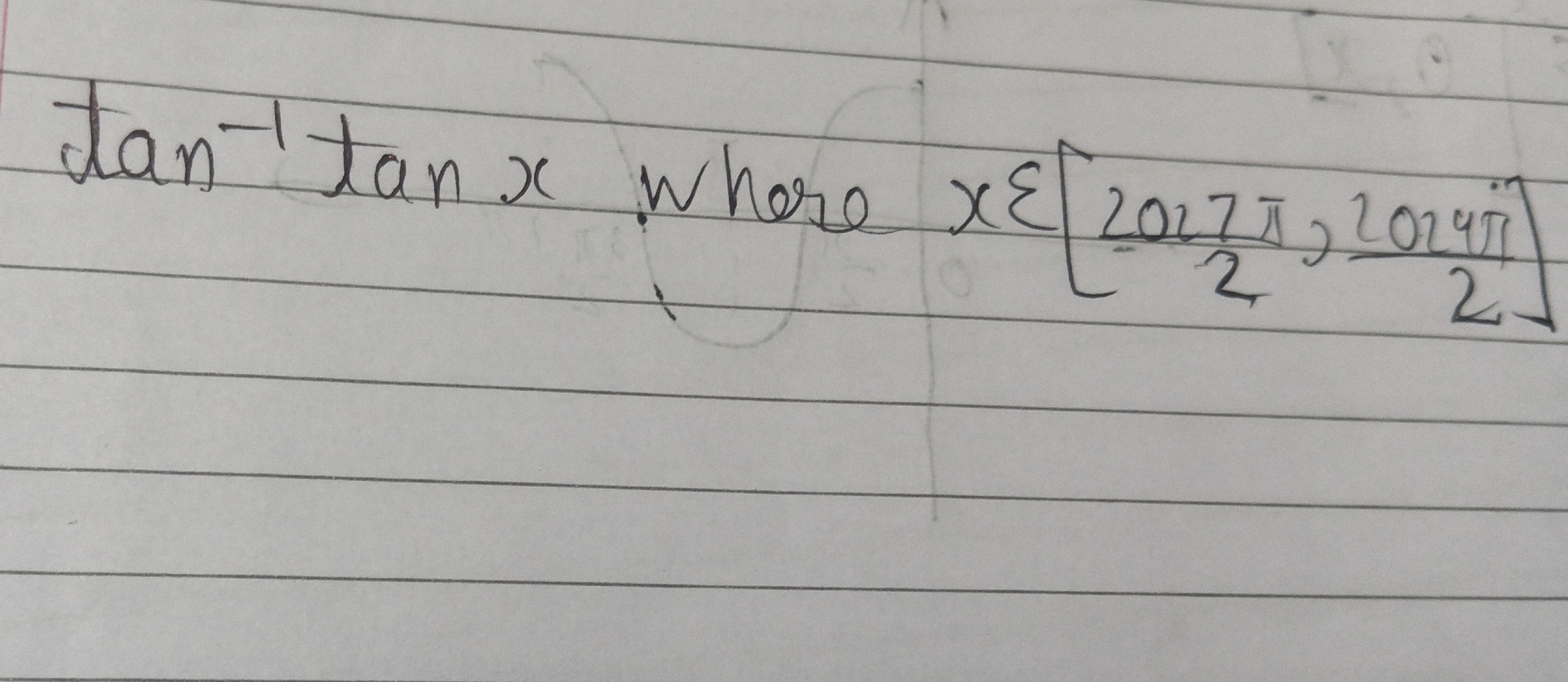
Answer
x-1014\pi
Explanation
Solution
We know that
tan−1(tanx)=x−nπ,where n is chosen so that x−nπ∈(−2π,2π).Given x∈[22027π,22029π], note that:
22027π=1013.5πand22029π=1014.5π.Choosing n=1014 gives:
x−1014π∈[1013.5π−1014π,1014.5π−1014π]=[−2π,2π].Thus, for every x in the interval, we have:
tan−1(tanx)=x−1014π.Since tan is periodic with period π, select n=1014 such that x−1014π∈[−2π,2π]. Therefore,
tan−1(tanx)=x−1014π.