Question
Question: $\tan^{-1}\frac{1}{\sqrt{x^2-1}}=$...
tan−1x2−11=
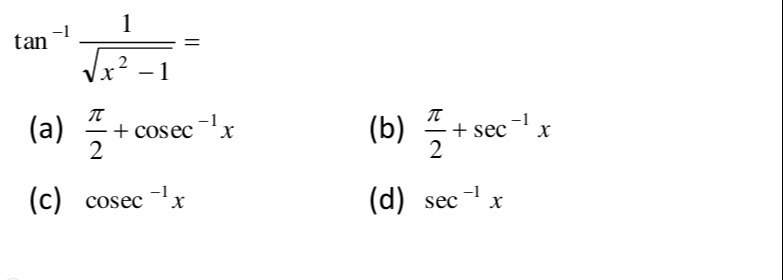
2π+cosec−1x
2π+sec−1x
cosec−1x
sec−1x
cosec−1x
Solution
Let the expression be y=tan−1x2−11. The domain of the expression is ∣x∣>1.
Case 1: x>1. Substitute x=secθ, where θ∈(0,π/2). y=tan−1sec2θ−11=tan−1tan2θ1=tan−1tanθ1=tan−1(cotθ)=tan−1(tan(π/2−θ)). Since θ∈(0,π/2), π/2−θ∈(0,π/2), which is in the range of tan−1. So, y=π/2−θ. Since x=secθ, θ=sec−1x. y=π/2−sec−1x. For x>1, cosec−1x+sec−1x=π/2, so π/2−sec−1x=cosec−1x. Thus, for x>1, y=cosec−1x.
Case 2: x<−1. Substitute x=secθ, where θ∈(π/2,π). y=tan−1sec2θ−11=tan−1tan2θ1=tan−1−tanθ1=tan−1(−cotθ)=tan−1(tan(θ−π/2)). Since θ∈(π/2,π), θ−π/2∈(0,π/2), which is in the range of tan−1. So, y=θ−π/2. Since x=secθ, θ=sec−1x. y=sec−1x−π/2. For x<−1, cosec−1x+sec−1x=π/2, so π/2−sec−1x=cosec−1x, or sec−1x−π/2=−cosec−1x. Thus, for x<−1, y=−cosec−1x.
Since option (c) cosec−1x matches the result for x>1, and is one of the given options, we choose it, assuming the question implicitly refers to the case x>1 or accepts partial matching.
