Question
Question: $\tan^{-1} 2x + \tan^{-1} 3x = \frac{\pi}{4}$, then x =...
tan−12x+tan−13x=4π, then x =
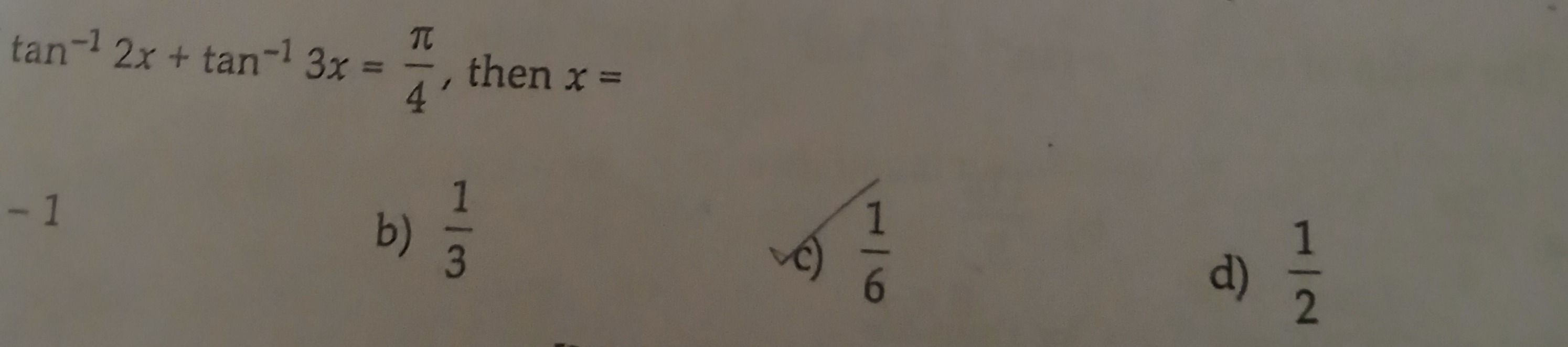
-1
31
61
21
61
Solution
To solve the equation tan−12x+tan−13x=4π, we use the formula for the sum of arctangents:
tan−1a+tan−1b=tan−1(1−aba+b)
In this case, a=2x and b=3x. Substituting these values into the formula, we get:
tan−1(1−6x22x+3x)=4π
Since tan(4π)=1, we have:
1−6x25x=1
Now, we solve the equation:
5x=1−6x2 6x2+5x−1=0
Using the quadratic formula:
x=2⋅6−5±52−4⋅6⋅(−1)=12−5±25+24=12−5±7
This gives us two possible solutions:
x=122=61 or x=12−12=−1
We need to check the validity of these solutions.
For x=61, (2x)(3x)=31⋅21=61<1, which satisfies the condition for the arctangent sum formula.
For x=−1, (2(−1))(3(−1))=6>1, and substituting in the original expression does not yield 4π.
Therefore, the valid solution is x=61.
