Question

Taken on side $\overline{AC}$ of a triangle $ABC$, a point $M$ such that $\overline{AM}=\dfrac{1}{3}\overline{AC}$. A point $N$ is taken on the side $\overline{CB}$ such that $\overline{BN}=\overline{CB}$, then for the point of intersection $X$ of $\overline{AB}$ and $\overline{MN}$ which of the following holds good?
(A) $\overline{XB}=\dfrac{1}{3}\overline{AB}$
(B) $\overline{AX}=\dfrac{1}{3}\overline{AB}$
(C) $\overline{XN}=\dfrac{3}{4}\overline{MN}$
(D) $\overline{XM}=3\overline{XN}$

Answer 1

To find out which relation holds for the given triangle we will use Ratio Rule. Firstly we will form the triangle and mark all the points given in it. Then we will let each side be a vector and try to form a relation between the points and get some equation related to them. Finally we will compare those equations and get our desired answer.

Complete step by step answer:
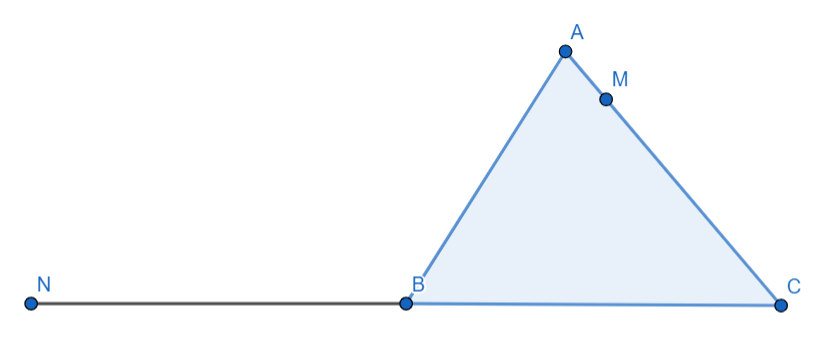
So it is given that we have a triangle $ABC$ with a point $M$ on $\overline{AC}$ such that $\overline{AM}=\dfrac{1}{3}\overline{AC}$ and point $N$ is taken on the side $\overline{CB}$ such that $\overline{BN}=\overline{CB}$ so we get the diagram as follows:

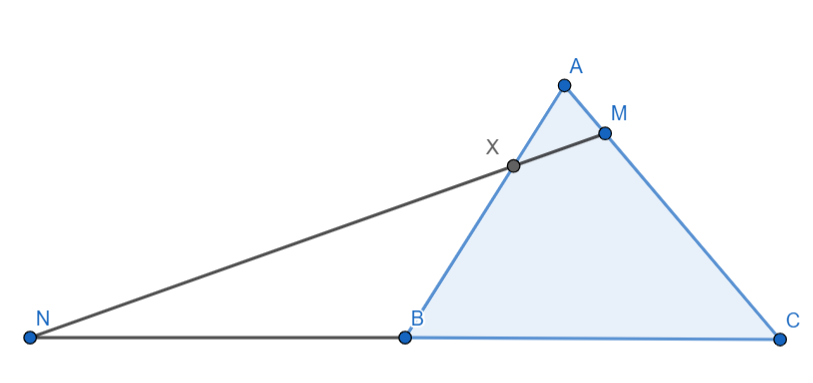
Next it is given that the point of intersection of $\overline{AB}$ and $\overline{MN}$ is $X$ so we get the diagram as:

Now let us take all the point as a vector as follows:

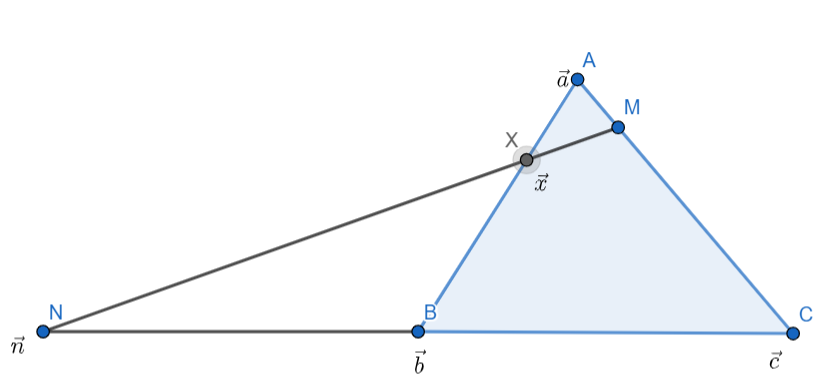
Now as it is given that $\overline{AM}=\dfrac{1}{3}\overline{AC}$ so we can say:
$AM:MC=1:2$…..$\left( 1 \right)$
Also as point $N,B,C$ is in straight line and also $\overline{BN}=\overline{CB}$ so we can say that:
$\overrightarrow{n}=-\overrightarrow{c}$…..$\left( 2 \right)$
So by using equation (1) we will get the coordinate of $\overrightarrow{M}$ using Ratio Rule as follows:
$\overrightarrow{M}=\dfrac{2\times \overrightarrow{a}+1\times \overrightarrow{c}}{2+1}$
$\overrightarrow{M}=\dfrac{2\overrightarrow{a}+\overrightarrow{c}}{3}$…..$\left( 3 \right)$
Next as we know $X$ lies in $A$ so we can let as below:
$\overrightarrow{X}=\gamma \overrightarrow{a}$…..$\left( 4 \right)$
Now we will let that $X$ point divide line $MN$ in $\lambda :1$ such that $NX=\lambda$, $XM=1$so using ratio test we get the coordinates of $\overrightarrow{X}$ as follows:
$\overrightarrow{X}=\dfrac{\lambda \overrightarrow{M}-\overrightarrow{N}}{\lambda +1}$
Put value from equation (2), (3) and (4) above and simplify to get,
$\begin{aligned} & \gamma \overrightarrow{a}=\dfrac{\lambda \times \dfrac{2\overrightarrow{a}+\overrightarrow{c}}{3}-\overrightarrow{c}}{\lambda +1} \\\ & \Rightarrow \gamma \overrightarrow{a}=\dfrac{\dfrac{2\lambda \overrightarrow{a}}{3}+\dfrac{\lambda \overrightarrow{c}}{3}-\overrightarrow{c}}{\lambda +1} \\\ & \Rightarrow \gamma \overrightarrow{a}=\dfrac{2\lambda \overrightarrow{a}}{3}+\overrightarrow{c}\left( \dfrac{\lambda }{3}-1 \right) \\\ \end{aligned}$
On comparing coefficient of $\overrightarrow{c}$ both side we get,
$\begin{aligned} & \left( \dfrac{\lambda }{3}-1 \right)=0 \\\ & \Rightarrow \dfrac{\lambda }{3}=1 \\\ & \Rightarrow \lambda =3\times 1 \\\ & \therefore \lambda =3 \\\ \end{aligned}$
Which means $X$ point divide line $MN$ in $3:1$.
So we can say that
$\overline{XN}=\dfrac{3}{4}\overline{MN}$
So, the correct answer is “Option C”.

Note: In these types of questions we always try to form the relation between the points on any side of the triangle with the vector point of that triangle. Ratio rule is used to make the calculation easy and using it we get the relation among the vector points.