Question
Question: If $\alpha_1 < \alpha_2 < \alpha_3 < \alpha_4 < \alpha_5 < \alpha_6$, then the equation $(x - \alpha...
If α1<α2<α3<α4<α5<α6, then the equation (x−α1)(x−α3)(x−α5)+3(x−α2)(x−α4)(x−α6)=0 has :-
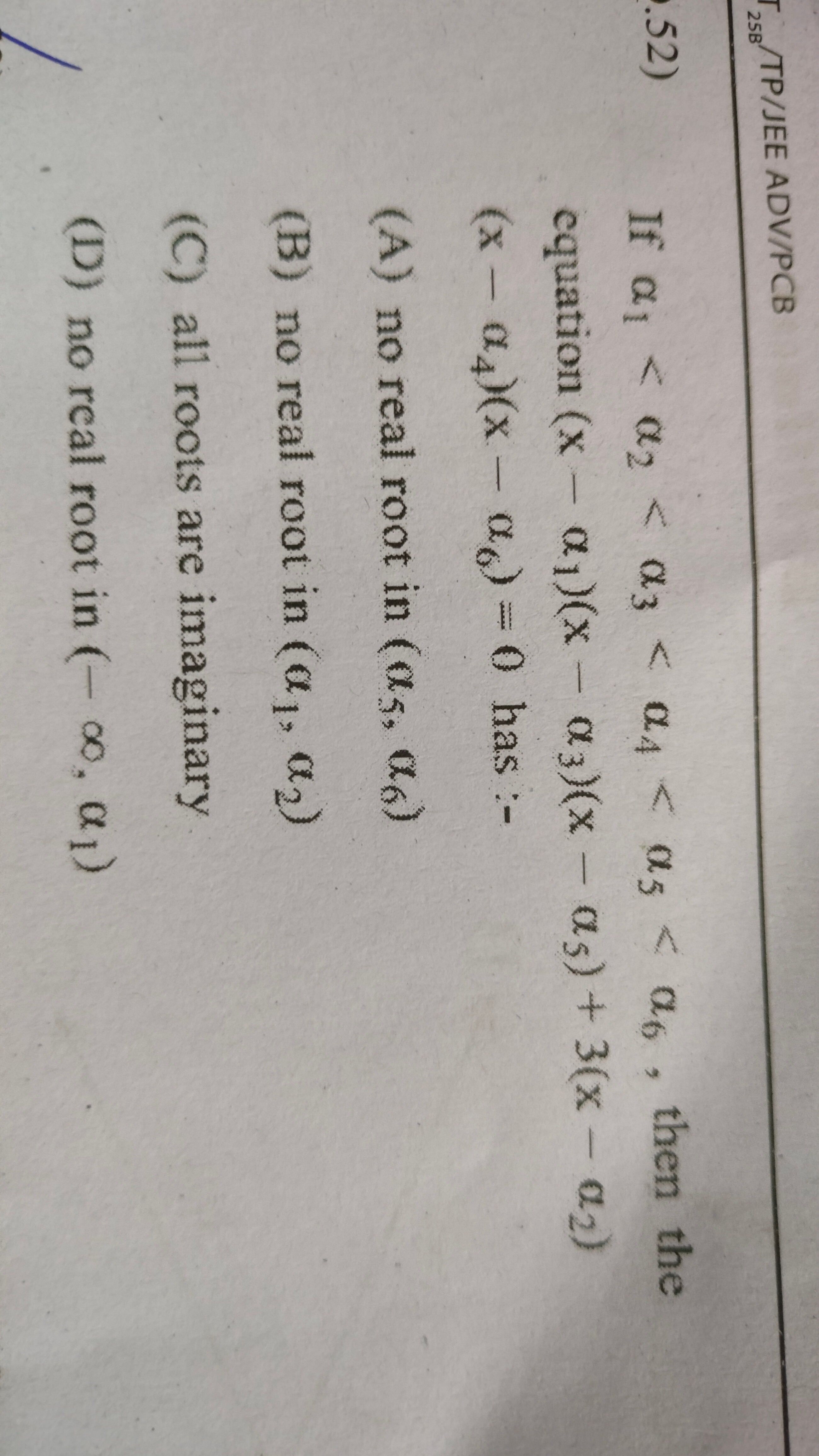
no real root in (α5,α6)
no real root in (α1,α2)
all roots are imaginary
no real root in (−∞,α1)
(D) no real root in (−∞,α1).
Solution
Explanation:
Let
Evaluate f(x) at the points where one of the factors becomes zero:
-
At x=α1:
f(α1)=0+3(α1−α2)(α1−α4)(α1−α6)Since α1<α2,α4,α6, each difference is negative so their product is negative. Thus, f(α1)<0.
-
At x=α2:
f(α2)=(α2−α1)(α2−α3)(α2−α5)+0Here (α2−α1)>0 and (α2−α3),(α2−α5)<0. The product of one positive and two negatives is positive. Hence, f(α2)>0.
By the Intermediate Value Theorem, there is a root in (α1,α2). -
Similarly, one finds a sign change (and hence a root) in (α3,α4) and in (α5,α6).
-
For x<α1, all factors (x−αi) are negative. Thus, each product (being the product of three negatives) is negative. Their sum is negative, and no sign change occurs from −∞ to α1.
