Question
Question: System is shown in figure and wedge is moving towards left with speed 2 m/s. Then velocity of the bl...
System is shown in figure and wedge is moving towards left with speed 2 m/s. Then velocity of the block B will be:
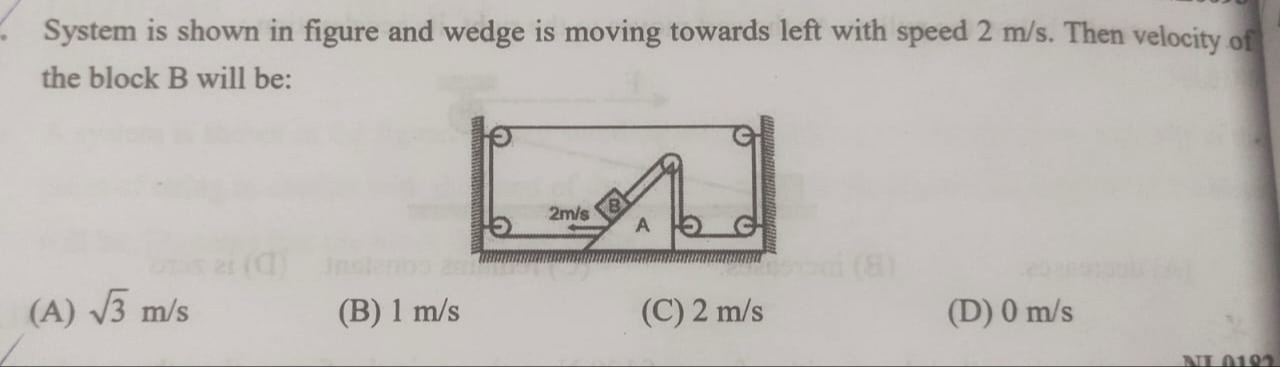
3 m/s
1 m/s
2 m/s
0 m/s
2 m/s
Solution
To determine the velocity of block B, we will use the principle of constant string length and vector addition of velocities.
1. Analyze the String Constraint:
Let L be the total length of the string. The string consists of several segments:
- Segment 1: From block B to pulley P1 (on the wedge A). Let its length be l1.
- Segment 2: From pulley P1 to pulley P2 (fixed on the right wall). Let its length be l2.
- Segment 3: From pulley P2 to pulley P3 (fixed on the right wall). Let its length be l3.
- Segment 4: From pulley P3 to the left wall (fixed). Let its length be l4.
The total length of the string is constant: L=l1+l2+l3+l4. Since pulleys P2 and P3 are fixed, and the string ends are fixed to the walls, the lengths l3 and l4 are constant. Therefore, differentiating the total length with respect to time:
dtdL=dtdl1+dtdl2+dtdl3+dtdl4=0.
Since dtdl3=0 and dtdl4=0, we have:
dtdl1+dtdl2=0.
Let xP1 be the horizontal position of pulley P1 and xP2 be the horizontal position of pulley P2. The segment l2 is horizontal, so l2=xP2−xP1. Differentiating l2: dtdl2=dtdxP2−dtdxP1. Since P2 is fixed, dtdxP2=0. So, dtdl2=−dtdxP1.
Substituting this into the earlier equation:
dtdl1−dtdxP1=0.
dtdl1=dtdxP1.
The wedge A is moving towards the left with a speed of 2 m/s. Pulley P1 is on the wedge A, so its horizontal velocity is the same as the wedge's velocity. Let's define the positive x-direction to the right. The velocity of the wedge A is vA=−2i^ m/s. So, dtdxP1=−2 m/s. Therefore, dtdl1=−2 m/s.
This means the length of the string segment l1 (from block B to pulley P1) is decreasing at a rate of 2 m/s. This implies that block B is moving towards pulley P1 along the incline with a speed of 2 m/s. In other words, the magnitude of the velocity of block B relative to wedge A, along the incline, is vB/A=2 m/s. Since l1 is decreasing, block B is moving up the incline.
2. Vector Addition of Velocities:
The absolute velocity of block B, vB, is the vector sum of its velocity relative to the wedge A, vB/A, and the velocity of the wedge A, vA.
vB=vB/A+vA.
We have vA=−2i^ m/s.
Let θ be the angle of inclination of the wedge with the horizontal. From the diagram, the incline appears to be at 60∘ to the horizontal. This is a common angle in physics problems when not explicitly stated but implied by the visual representation (e.g., an equilateral triangle-like shape for the wedge's incline). Let's assume θ=60∘.
Block B is moving up the incline relative to A with a speed of 2 m/s. The incline goes up and to the right. So, the x-component of vB/A is vB/Acosθ=2cosθ. The y-component of vB/A is vB/Asinθ=2sinθ. Thus, vB/A=(2cosθ)i^+(2sinθ)j^.
Now, substitute the values into the vector sum:
vB=(2cosθ)i^+(2sinθ)j^+(−2i^)
vB=(2cosθ−2)i^+(2sinθ)j^.
Now, substitute θ=60∘:
cos60∘=21
sin60∘=23
vB=(2⋅21−2)i^+(2⋅23)j^
vB=(1−2)i^+(3)j^
vB=−1i^+3j^.
The magnitude of the velocity of block B is:
∣vB∣=(−1)2+(3)2
∣vB∣=1+3
∣vB∣=4
∣vB∣=2 m/s.
This matches option (C).
Explanation of the solution:
The problem involves a system with a wedge and a block connected by a string over pulleys. By applying the constraint of constant string length, it's found that the block B moves up the incline relative to the wedge A with a speed equal to the speed of the wedge (2 m/s). The absolute velocity of block B is then determined by vectorially adding its relative velocity to the velocity of the wedge. Assuming the incline angle is 60∘ (a common implied angle in such diagrams), the components of relative velocity are calculated. Summing these with the wedge's velocity yields the total velocity of block B, whose magnitude is 2 m/s.
