Question

Switch S is closed at $t = 0$ , ${I_{10}}$ is the current supplied by the battery just after closing the switch S. ${Q_1}$ , ${Q_2}$ and ${Q_3}$ are the charges on the capacitors of $10\mu F$ , $20\mu F$ and $30\mu F$ in steady state respectively. ${I_{20}}$ is the current supplied by the battery in the circuit at steady state. Choose the correct statement(s).

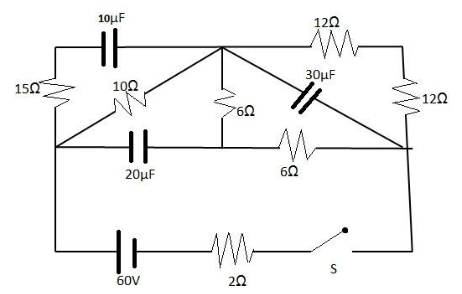
(A) ${I_{10}} > {I_{20}}$
(B) ${I_{10}} < {I_{20}}$
(C) ${Q_1} < {Q_2} < {Q_3}$
(D) ${Q_1} < {Q_3} < {Q_2}$

Answer 1

No current was flowing through the capacitors before the switch was closed at $t = 0$ . We know that current is the flow of charge.

Formula Used: The formulae used in the solution are given here.
Current $I = C\dfrac{{dV}}{{dt}}$ , where $C$ the capacitance in Farad and voltage across the capacitor is $V$ .
Charge on the capacitor, $Q = CV$ .

Complete Step by Step Solution
No flow of charge to and from the capacitors plates was zero, prior to $t = 0$ . Hence as charge on capacitor plates varies proportionally with the voltage across them, therefore voltage across them is zero before $t = 0$ . We can say that the capacitor was short circuited or it behaved as if it was being short circuited.
We know, current through capacitor, $I$ and voltage across the capacitor, $V$ , is related as
$I = C\dfrac{{dV}}{{dt}}$ , where $C$ is the capacitance in Farad.
Following from the above, when the switch is turned on at $t = 0$ , the capacitor behaves as being short circuited , for the initial time being.
The circuit thus looks like,

On solving, we see that the resistances $10\Omega$ , $6\Omega$ , $15\Omega$ , $6\Omega$ are in parallel. So equivalent resistance,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{10}} + \dfrac{1}{6} + \dfrac{1}{{15}} + \dfrac{1}{6}$
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{2}$ .
So equivalent resistance, ${R_{eq}} = 2\Omega$ .
There is another resistance $2\Omega$ connected in series to the arrangement for which ${R_{eq}} = 2\Omega$ .
Thus, resistance $R = 4\Omega$ .
By Ohm’s Law, $V = IR$ .
Thus, ${I_{10}} = \dfrac{{60}}{4} = 15A$ .
At steady state, that is, after some time, the capacitor starts behaving like an open circuit.
Thus two $6\Omega$ resistors are in parallel with two $12\Omega$ resistors.
Equivalent resistance is thus,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{2 \times 6}} + \dfrac{1}{{2 \times 12}}$
$\Rightarrow \dfrac{1}{{{R_{eq}}}} = \dfrac{1}{8}$
S, equivalent resistance ${R_{eq}} = 8\Omega$ .
There are two resistances $10\Omega$ and $2\Omega$ connected in series to the arrangement for which ${R_{eq}} = 8\Omega$
By Ohm’s Law, $V = IR$ .
At ${I_{20}} = \dfrac{{60}}{{20}} = 3A.$
So ${I_{20}} > {I_{10}}$ .
Hence Option A is correct.
Now charge on the capacitor, $Q = CV$ .
Voltage across the $10\mu F$ capacitor at steady state= $30V$ .
${Q_1} = 10\mu F \times 30$ .
Voltage across the $20\mu F$ capacitor at steady state= $30V$ .
${Q_2} = 20\mu F \times 42$ .
Voltage across the $30\mu F$ capacitor at steady state= $30V$ .
${Q_3} = 30\mu F \times 24$ .
It is quite apparent, ${Q_3} > {Q_2} > {Q_1}$ .
Hence Option D is also correct.

Note:
We can conclude that if voltage changes abruptly, current through the capacitor is spiked up. So, the tendency of the capacitor is to avoid the abrupt change in voltage across it.