Question

Switch ${{S}_{1}}$ is closed for a long time while ${{S}_{2}}$ remains open. Now at t=0, ${{S}_{2}}$ is closed while ${{S}_{1}}$ is opened. All the batteries are ideal and connecting wires are resistance-less. The capacitor C is initially uncharged.

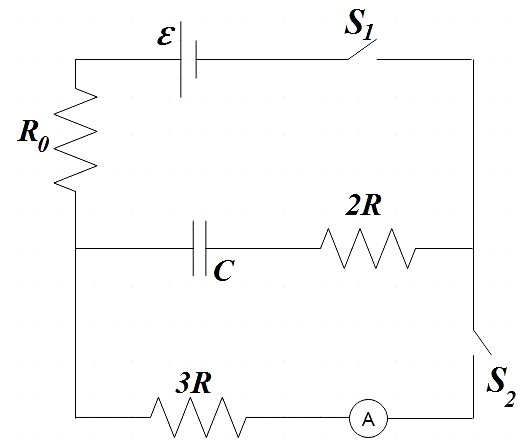
A. At time t=0, reading of ammeter is $\dfrac{\varepsilon }{5R}$
B. At time t=0, reading of ammeter is zero.
C. Heat developed till time $t=RC\ln 2$ in resistance 3R is $\dfrac{9}{40}C{{\varepsilon }^{2}}$
D. After time t > 0 charge on the capacitor follows the equation $C\varepsilon {{e}^{\dfrac{t}{5RC}}}$

Answer 1

When ${{S}_{1}}$ closed with ${{S}_{2}}$ open, the capacitor develops a potential difference of $\varepsilon$ and when the ${{S}_{2}}$ closed with ${{S}_{1}}$ open at t =0, then the capacitor starts discharging. You could find the effective resistance in the circuit and then apply ohm’s law to find the current. Then recall the expression for charge stored in a capacitor at time t and do necessary substitutions to get the charge in the given capacitor at t>0. Using the above charge, find the energy stored at a given time t and then find the difference in energy stored from t=0 to t=t to find the heat developed. And then find heat developed by resistance 3R.

Formula used:
Ohm’s law,
$V=IR$
Charge at time t,
$q={{q}_{0}}{{e}^{-\dfrac{t}{\tau }}}$
Energy stored in a capacitor,
$E=\dfrac{1}{2}C{{V}^{2}}$

Complete step-by-step answer:
When switch ${{S}_{1}}$ is closed with ${{S}_{2}}$ open, after a longtime, the capacitor in circuit gets fully charged with potential difference equal to that in the cell.

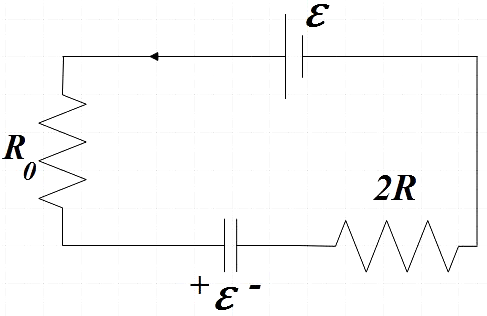
Now when the switch ${{S}_{1}}$ is kept open with ${{S}_{2}}$ turned on at t = 0, the capacitor starts discharging.

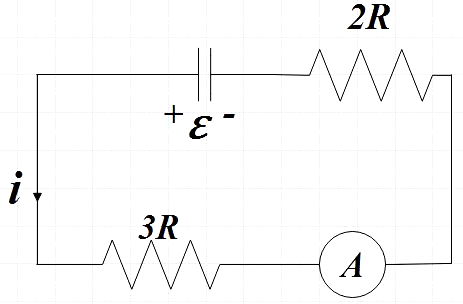
The charge in the capacitor at t =0 will be,
$Q=C\varepsilon$ …………………………….. (1)
From ohm’s law we know that,
$I=\dfrac{V}{R}$
Where R is the effective resistance of the given circuit,
$R=2R+3R=5R$ ……………………………… (2)
$\Rightarrow i=\dfrac{E}{5R}$ …………………………... (3)
Therefore option A is true.
We know that charge stored in a discharging capacitor at a time t is given by,
$q={{q}_{0}}{{e}^{-\dfrac{t}{\tau }}}$
Where, $\tau =RC$
For the given circuit, charge in the capacitor at t using (1) and (2) is given by,
$q=\left( C\varepsilon \right){{e}^{\dfrac{-t}{5RC}}}$ …………………………… (4)
Therefore option D is true.
When, $t=5RC\ln 2$
$q=C\varepsilon {{e}^{\dfrac{-5RC\ln 2}{5RC}}}$
$\Rightarrow q=C\varepsilon {{e}^{-\ln 2}}=C\varepsilon {{e}^{\ln \left( {{2}^{-1}} \right)}}$
But we know, ${{e}^{\ln x}}=x$
So, charge stored in the capacitor at time $t=5RC\ln 2$ is given by,
$q=\dfrac{C\varepsilon }{2}$
Energy stored by the capacitor at t =0 is,
${{E}_{i}}=\dfrac{1}{2}C{{\varepsilon }^{2}}$
Charged stored by capacitor at $t=5RC\ln 2$ will be,
${{E}_{f}}=\dfrac{1}{2}\dfrac{{{q}^{2}}}{C}$
$\Rightarrow {{E}_{f}}=\dfrac{1}{2}\dfrac{{{\left( \dfrac{1}{2}C\varepsilon \right)}^{2}}}{C}=\dfrac{1}{8}C{{\varepsilon }^{2}}$
The change energy from t =0 to $t=5RC\ln 2$ gives the heat total developed during that interval,
$\Delta E={{E}_{i}}-{{E}_{f}}=\dfrac{1}{8}C{{\varepsilon }^{2}}-\dfrac{1}{2}C{{\varepsilon }^{2}}=\dfrac{3}{8}C{{\varepsilon }^{2}}$
Heat developed across just the 3R resistor is given by,
${{H}_{3R}}=\dfrac{3}{8}C{{\varepsilon }^{2}}\times \dfrac{3}{5}$
$\Rightarrow {{H}_{3R}}=\dfrac{9}{40}C{{\varepsilon }^{2}}$
Therefore option C is also true.
Hence, we see that options A, C and D are true for a given situation.

So, the correct answers are “Option A, C and D”.

Note: In questions like this where we have to find the true statements among the given ones, we should check all the options one by one and then declare the correct answer. Chances are there for multiple options being true. So even when you find the very first option as true, you must check for the true statement in the other options too.