Question
Question: rth term in the expansion of $(a+2x)^n$ is ...
rth term in the expansion of (a+2x)n is
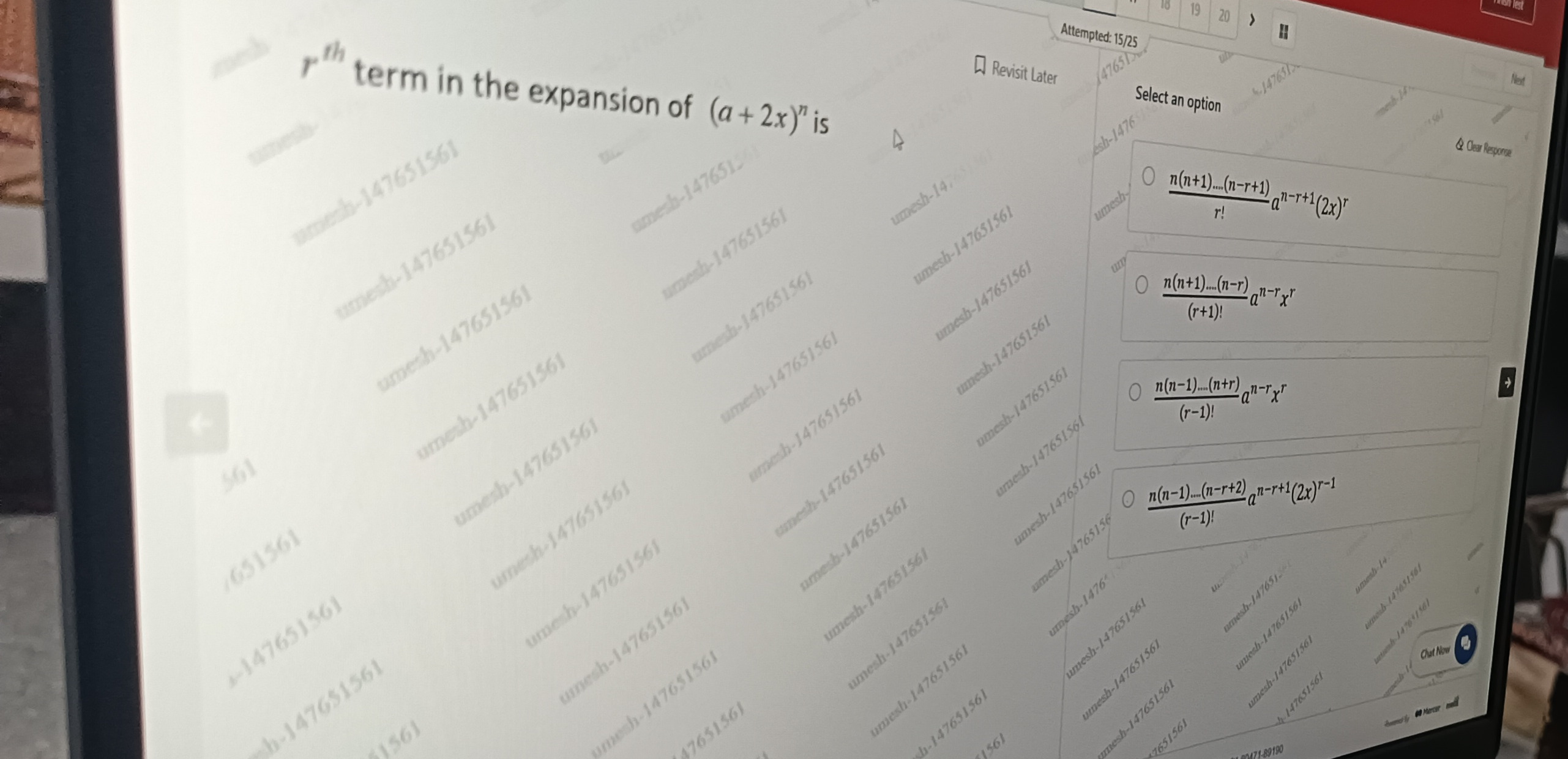
r!n(n+1)....(n−r+1)an−r+1(2x)r
(r+1)!n(n+1)....(n−r)an−rxr
(r−1)!n(n−1)....(n+r)an−rxr
(r−1)!n(n−1)...(n−r+2)an−r+1(2x)r−1
(r−1)!n(n−1)...(n−r+2)an−r+1(2x)r−1
Solution
The general term in the binomial expansion of (X+Y)n is given by Tk+1=(kn)Xn−kYk.
In the given problem, we have the expansion of (a+2x)n. Here, X=a and Y=2x. We need to find the rth term, which means Tr. To find Tr, we set k+1=r, which implies k=r−1.
Substitute k=r−1, X=a, and Y=2x into the general term formula: Tr=(r−1n)an−(r−1)(2x)r−1 Tr=(r−1n)an−r+1(2x)r−1
Now, let's express the binomial coefficient (r−1n) in expanded form: (r−1n)=(r−1)!(n−(r−1))!n!=(r−1)!(n−r+1)!n!
To match the form presented in the options, we can write n! as a product of terms: n!=n×(n−1)×(n−2)×⋯×(n−r+2)×(n−r+1)!
Substitute this back into the expression for (r−1n): (r−1n)=(r−1)!(n−r+1)!n(n−1)(n−2)…(n−r+2)(n−r+1)! (r−1n)=(r−1)!n(n−1)(n−2)…(n−r+2)
Finally, substitute this back into the expression for Tr: Tr=(r−1)!n(n−1)(n−2)…(n−r+2)an−r+1(2x)r−1
Comparing this result with the given options, we find that it matches the fourth option.
