Question

Supposethat w = $2^{1/2}$, x = $3^{1/3}$, y = $6^{1/6}$ and z = $8^{1/8}$. From among these number list, the biggest, second biggest numbers are

Answer 1

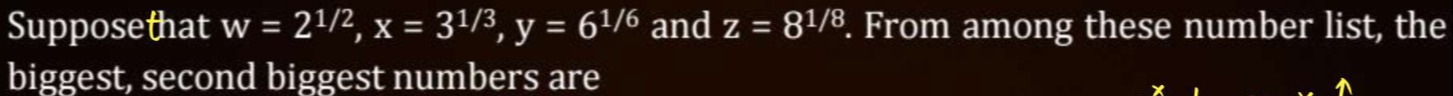
$3^{1/3}, 2^{1/2}$

Answer 2

To compare the given numbers $w = 2^{1/2}$, $x = 3^{1/3}$, $y = 6^{1/6}$, and $z = 8^{1/8}$, we raise each number to a common power that eliminates the fractional exponents. This common power is the Least Common Multiple (LCM) of the denominators of the exponents (2, 3, 6, and 8).

The LCM of 2, 3, 6, and 8 is 24.

Now, we raise each number to the power of 24:

1. For $w = 2^{1/2}$: $w^{24} = (2^{1/2})^{24} = 2^{(1/2) \times 24} = 2^{12}$ $2^{12} = 4096$

2. For $x = 3^{1/3}$: $x^{24} = (3^{1/3})^{24} = 3^{(1/3) \times 24} = 3^8$ $3^8 = (3^4)^2 = 81^2 = 6561$

3. For $y = 6^{1/6}$: $y^{24} = (6^{1/6})^{24} = 6^{(1/6) \times 24} = 6^4$ $6^4 = (6^2)^2 = 36^2 = 1296$

4. For $z = 8^{1/8}$: $z^{24} = (8^{1/8})^{24} = 8^{(1/8) \times 24} = 8^3$ $8^3 = 512$

Now, we compare the calculated values: $x^{24} = 6561$ $w^{24} = 4096$ $y^{24} = 1296$ $z^{24} = 512$

Arranging these values in descending order: $6561 > 4096 > 1296 > 512$

This implies the order of the original numbers from biggest to smallest is: $x > w > y > z$

Therefore, the biggest number is $x = 3^{1/3}$ and the second biggest number is $w = 2^{1/2}$.