Question

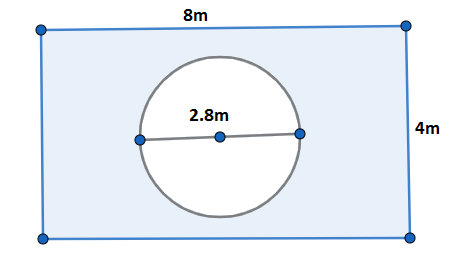
Suppose you drop a die at random on the rectangular region shown in figure. What is the probability that it will land inside the circle with diameter 2.8m? $$$$

Answer 1

We find the probability of the die landing inside the circle $P\left( A \right)=\dfrac{n\left( A \right)}{n\left( S \right)}$ where $n\left( A \right)$ the area of the circle is calculated as $\pi {{r}^{2}}$ where $r$ is the radius half of diameter 2.8m and $n\left( S \right)$ is the area of rectangle calculated by multiplying given length 8m into breadth 4m from the figure. $$$$

Complete step-by-step answer:
We know from definition of probability that if there is $n\left( A \right)$ number of ways of event $A$ occurring (or number of favourable outcomes) and $n\left( S \right)$ is the size of the sample space (number of all possible outcomes) then the probability of the event $A$ occurring is given by
$P\left( A \right)=\dfrac{n\left( A \right)}{n\left( S \right)}$
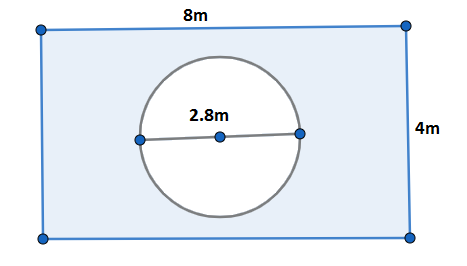
We are given that die has to be dropped at random on the rectangular region in the given figure and are asked to find out the probability that die will land inside the circle with diameter 2.8m.  Let us denote the event of die landing inside the circle as $A$. Now every point inside the circle becomes a favourable outcome and every point inside the rectangle becomes a possible outcome but we cannot count the number of points. So take the interior of the circle as a favourable outcome and the interior of the rectangle becomes all possible outcomes. We can represent the amount of interior with area.
We know that the area of the circle is $\pi {{r}^{2}}$ where $r$ is the radius. We are given the diameter 2.8. So the radius is half of diameter which is $r=\dfrac{2.8}{2}=1.4$ m. So the area of the circle is number of favourable outcome as
$n\left( A \right)=\pi {{r}^{2}}=\pi {{\left( 1.4 \right)}^{2}}=1.96\pi \text{ }{{\text{m}}^{2}}$
We know that the area of the rectangle is length times breadth. We are given in the figure length as 8m and breadth as 4m. So the area of the rectangle as the number of possible outcome is
$n\left( S \right)=8\times 4=32\text{ }{{\text{m}}^{2}}$
So the required probability of event $A$ is,
$P\left( A \right)=\dfrac{n\left( A \right)}{n\left( S \right)}=\dfrac{1.96\pi }{32}=\dfrac{.49\pi }{8}=\dfrac{49}{800}\pi$

Note: We note that when the question says ‘random’ it means previously it was not designed to favour the landing of the die in the circle like making a circular region with more depth than the rectangular region. We also assume that the boundary circle is so thin; the die will not land on the circle. We can find the probability of not landing the circle as $1-P\left( A \right)$.