Solveeit Logo
Login

Question

Question: Suppose you are anchored near the shore of a channel in which there is steady current, and you are g...

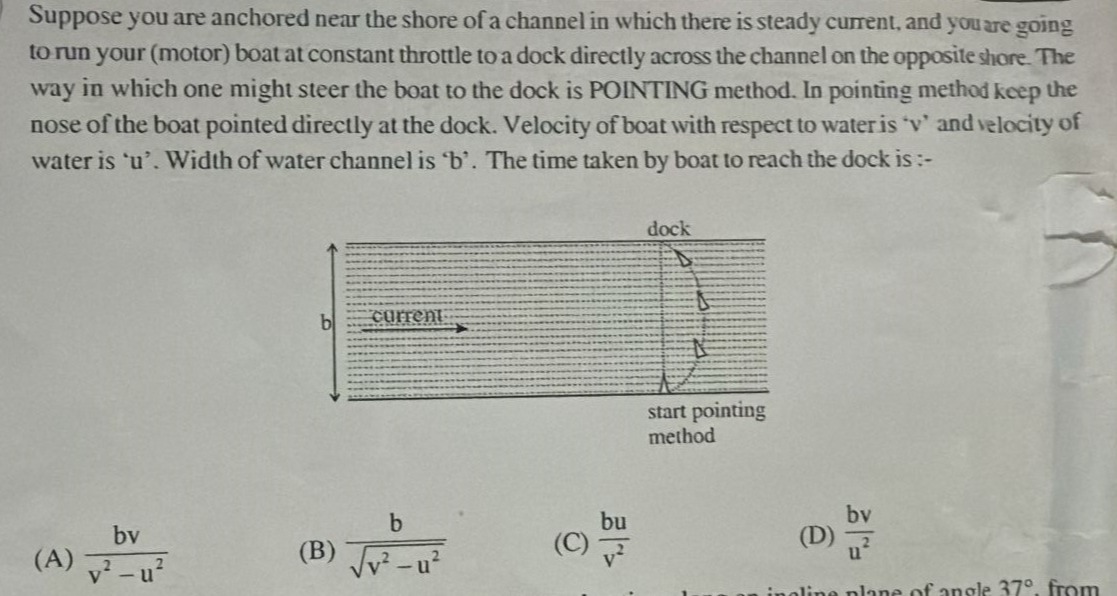
Suppose you are anchored near the shore of a channel in which there is steady current, and you are going to run your (motor) boat at constant throttle to a dock directly across the channel on the opposite shore. The way in which one might steer the boat to the dock is POINTING method. In pointing method keep the nose of the boat pointed directly at the dock. Velocity of boat with respect to water is 'v' and velocity of water is 'u'. Width of water channel is 'b'. The time taken by boat to reach the dock is :-

A

bvv2−u2\frac{bv}{v^2-u^2}

B

bv2−u2\frac{b}{\sqrt{v^2-u^2}}

C

buv2\frac{bu}{v^2}

D

bvu2\frac{bv}{u^2}

Answer

bvv2−u2\frac{bv}{v^2-u^2}

Explanation

Solution

Let the starting point of the boat be the origin (0, 0) and the dock be at (0, b). The river flows in the positive x-direction with velocity u⃗=ui^\vec{u} = u \hat{i}. The velocity of the boat with respect to water is v⃗bw\vec{v}_{bw}, with magnitude vv. The boat is always pointed towards the dock. Let the instantaneous position of the boat be (x,y)(x, y). The vector from the boat to the dock is r⃗bd=(0−x)i^+(b−y)j^=−xi^+(b−y)j^\vec{r}_{bd} = (0 - x) \hat{i} + (b - y) \hat{j} = -x \hat{i} + (b - y) \hat{j}. The direction of v⃗bw\vec{v}_{bw} is along r⃗bd\vec{r}_{bd}.

So, v⃗bw=vr⃗bd∣r⃗bd∣=v−xi^+(b−y)j^x2+(b−y)2\vec{v}_{bw} = v \frac{\vec{r}_{bd}}{|\vec{r}_{bd}|} = v \frac{-x \hat{i} + (b - y) \hat{j}}{\sqrt{x^2 + (b - y)^2}}.

The velocity of the boat with respect to the ground is v⃗b=v⃗bw+v⃗w\vec{v}_b = \vec{v}_{bw} + \vec{v}_w. v⃗b=v−xi^+(b−y)j^x2+(b−y)2+ui^\vec{v}_b = v \frac{-x \hat{i} + (b - y) \hat{j}}{\sqrt{x^2 + (b - y)^2}} + u \hat{i}. The components of the boat's velocity are: dxdt=vx=u−vxx2+(b−y)2\frac{dx}{dt} = v_x = u - \frac{vx}{\sqrt{x^2 + (b - y)^2}} dydt=vy=v(b−y)x2+(b−y)2\frac{dy}{dt} = v_y = \frac{v(b - y)}{\sqrt{x^2 + (b - y)^2}}

Let r=x2+(b−y)2r = \sqrt{x^2 + (b-y)^2} be the distance from the boat to the dock. Consider the rate of change of the distance from the boat to the dock. The velocity of the boat relative to the dock is v⃗b−v⃗d\vec{v}_b - \vec{v}_d. Since the dock is stationary, v⃗d=0\vec{v}_d = 0, so the velocity of the boat relative to the dock is v⃗b\vec{v}_b. The rate of change of the distance rr is the component of v⃗b\vec{v}_b in the direction from the boat to the dock (which is the direction of −r⃗bd-\vec{r}_{bd}). drdt=v⃗b⋅(−r⃗bd∣r⃗bd∣)=(vr⃗bd∣r⃗bd∣+ui^)⋅(−r⃗bd∣r⃗bd∣)=−v(r⃗bd∣r⃗bd∣⋅r⃗bd∣r⃗bd∣)−u(i^⋅r⃗bd∣r⃗bd∣)\frac{dr}{dt} = \vec{v}_b \cdot \left(-\frac{\vec{r}_{bd}}{|\vec{r}_{bd}|}\right) = \left(v \frac{\vec{r}_{bd}}{|\vec{r}_{bd}|} + u \hat{i}\right) \cdot \left(-\frac{\vec{r}_{bd}}{|\vec{r}_{bd}|}\right) = -v \left(\frac{\vec{r}_{bd}}{|\vec{r}_{bd}|} \cdot \frac{\vec{r}_{bd}}{|\vec{r}_{bd}|}\right) - u \left(\hat{i} \cdot \frac{\vec{r}_{bd}}{|\vec{r}_{bd}|}\right). drdt=−v(1)−u(i^⋅−xi^+(b−y)j^x2+(b−y)2)=−v−u−xx2+(b−y)2=−v+uxx2+(b−y)2\frac{dr}{dt} = -v (1) - u \left(\hat{i} \cdot \frac{-x \hat{i} + (b-y) \hat{j}}{\sqrt{x^2 + (b-y)^2}}\right) = -v - u \frac{-x}{\sqrt{x^2 + (b-y)^2}} = -v + \frac{ux}{\sqrt{x^2 + (b-y)^2}}.

This still depends on x and y. Let's look for a simpler approach. Consider the y-component of the velocity: dydt=v(b−y)x2+(b−y)2\frac{dy}{dt} = \frac{v(b-y)}{\sqrt{x^2 + (b-y)^2}}. Notice that x2+(b−y)2\sqrt{x^2 + (b-y)^2} is the distance rr from the boat to the dock. So, dydt=v(b−y)r\frac{dy}{dt} = \frac{v(b-y)}{r}. Also, drdt=−v+uxr\frac{dr}{dt} = -v + \frac{ux}{r}.

Let's consider the relationship between x and y. From the first equation, dxdt=u−vxr\frac{dx}{dt} = u - \frac{vx}{r}. We have dydt=v(b−y)r\frac{dy}{dt} = \frac{v(b-y)}{r}. Dividing the two equations: dxdy=u−vxrv(b−y)r=ur−vxv(b−y)\frac{dx}{dy} = \frac{u - \frac{vx}{r}}{\frac{v(b-y)}{r}} = \frac{ur - vx}{v(b-y)}. v(b−y)dxdy=ur−vxv(b-y) \frac{dx}{dy} = ur - vx. v(b−y)dxdy+vx=ur=ux2+(b−y)2v(b-y) \frac{dx}{dy} + vx = ur = u \sqrt{x^2 + (b-y)^2}.

This differential equation looks hard to solve. Let's consider the energy approach or some invariant.

Let's reconsider the y-component of velocity: dydt=v(b−y)x2+(b−y)2\frac{dy}{dt} = \frac{v(b-y)}{\sqrt{x^2+(b-y)^2}}. Let y=b−rcos⁡θy = b - r \cos \theta and x=rsin⁡θx = r \sin \theta, where θ\theta is the angle between the line from the boat to the dock and the negative y-axis. This might be complicated due to the moving coordinate system.

Let's go back to dydt=v(b−y)r\frac{dy}{dt} = \frac{v(b-y)}{r}. We also have drdt=−v+uxr\frac{dr}{dt} = -v + \frac{ux}{r}. From the figure, as the boat moves, x changes, and y changes. The boat starts at (0,0) and ends at (0,b). The y-component of the boat's velocity relative to the ground is vy=v(b−y)x2+(b−y)2v_y = \frac{v(b-y)}{\sqrt{x^2+(b-y)^2}}. Let's assume the boat reaches the dock at time T. We need to find T. T=∫0bdtdydy=∫0bx2+(b−y)2v(b−y)dyT = \int_0^b \frac{dt}{dy} dy = \int_0^b \frac{\sqrt{x^2+(b-y)^2}}{v(b-y)} dy. This integral still depends on x(y).

Let's consider a special case: if u=0, then dxdt=−vxx2+(b−y)2\frac{dx}{dt} = -\frac{vx}{\sqrt{x^2+(b-y)^2}} and dydt=v(b−y)x2+(b−y)2\frac{dy}{dt} = \frac{v(b-y)}{\sqrt{x^2+(b-y)^2}}. If the boat is pointed directly at the dock and there is no current, the boat moves along the straight line from (0,0) to (0,b) with speed v. The time taken would be b/v. Let's check the options for u=0. (A) bvv2−02=bv\frac{bv}{v^2-0^2} = \frac{b}{v}. (B) bv2−02=bv\frac{b}{\sqrt{v^2-0^2}} = \frac{b}{v}. (C) b⋅0v2=0\frac{b \cdot 0}{v^2} = 0. (D) bv02\frac{bv}{0^2}, undefined. So, options A and B are possible candidates.

Let's consider another approach. Let the angle that the line from the boat to the dock makes with the y-axis be α\alpha. So cos⁡α=b−yx2+(b−y)2\cos \alpha = \frac{b-y}{\sqrt{x^2+(b-y)^2}}. Then dydt=vcos⁡α\frac{dy}{dt} = v \cos \alpha. Also, sin⁡α=−xx2+(b−y)2\sin \alpha = \frac{-x}{\sqrt{x^2+(b-y)^2}}. dxdt=u+vsin⁡α=u−vxx2+(b−y)2\frac{dx}{dt} = u + v \sin \alpha = u - \frac{vx}{\sqrt{x^2+(b-y)^2}}.

Consider the case where v > u. If v <= u, the boat might not be able to reach the dock if the current is strong enough. The problem statement implies the boat reaches the dock. So, let's assume v > u.

This problem is a classic example of a pursuit curve. The boat is pursuing the dock.

Let's use the y-component of velocity: dydt=v(b−y)x2+(b−y)2\frac{dy}{dt} = \frac{v(b-y)}{\sqrt{x^2 + (b-y)^2}}. Let the distance from the boat to the dock be r=x2+(b−y)2r = \sqrt{x^2 + (b-y)^2}. dydt=v(b−y)r\frac{dy}{dt} = \frac{v(b-y)}{r}.

Consider the velocity component along the line joining the boat and the dock. The relative velocity of the boat with respect to the dock along the line joining them is the rate at which the distance between them decreases. The velocity of the boat is v⃗b=v⃗bw+u⃗\vec{v}_b = \vec{v}_{bw} + \vec{u}. The direction of v⃗bw\vec{v}_{bw} is towards the dock. Let r^\hat{r} be the unit vector from the boat to the dock. v⃗bw=vr^\vec{v}_{bw} = v \hat{r}. v⃗b=vr^+u⃗\vec{v}_b = v \hat{r} + \vec{u}. The rate of decrease of the distance rr is −drdt=v⃗b⋅r^=(vr^+u⃗)⋅r^=v(r^⋅r^)+u⃗⋅r^=v+u⃗⋅r^-\frac{dr}{dt} = \vec{v}_b \cdot \hat{r} = (v \hat{r} + \vec{u}) \cdot \hat{r} = v (\hat{r} \cdot \hat{r}) + \vec{u} \cdot \hat{r} = v + \vec{u} \cdot \hat{r}. Let θ\theta be the angle between r^\hat{r} and i^\hat{i}. Then u⃗⋅r^=ucos⁡θ\vec{u} \cdot \hat{r} = u \cos \theta. The vector from the boat (x,y)(x,y) to the dock (0,b)(0,b) is (−x,b−y)(-x, b-y). The angle θ\theta is the angle between (−x,b−y)(-x, b-y) and (1,0)(1, 0). cos⁡θ=(−x,b−y)⋅(1,0)x2+(b−y)2⋅1=−xx2+(b−y)2\cos \theta = \frac{(-x, b-y) \cdot (1, 0)}{\sqrt{x^2 + (b-y)^2} \cdot 1} = \frac{-x}{\sqrt{x^2 + (b-y)^2}}. So, −drdt=v+u−xx2+(b−y)2=v−uxx2+(b−y)2-\frac{dr}{dt} = v + u \frac{-x}{\sqrt{x^2 + (b-y)^2}} = v - \frac{ux}{\sqrt{x^2 + (b-y)^2}}. drdt=−v+uxx2+(b−y)2\frac{dr}{dt} = -v + \frac{ux}{\sqrt{x^2 + (b-y)^2}}. This matches our previous result.

Let's consider the y-component again: dydt=v(b−y)x2+(b−y)2\frac{dy}{dt} = \frac{v(b-y)}{\sqrt{x^2 + (b-y)^2}}. Let y=b−δy = b - \delta, where δ\delta is the remaining distance in the y-direction. d(b−δ)dt=vδx2+δ2\frac{d(b-\delta)}{dt} = \frac{v \delta}{\sqrt{x^2 + \delta^2}}. −dδdt=vδx2+δ2-\frac{d\delta}{dt} = \frac{v \delta}{\sqrt{x^2 + \delta^2}}.

Consider the relationship between x and δ\delta. dxdt=u−vxx2+δ2\frac{dx}{dt} = u - \frac{vx}{\sqrt{x^2 + \delta^2}}. dxdδ=u−vxx2+δ2−vδx2+δ2=ux2+δ2−vx−vδ=vx−ux2+δ2vδ\frac{dx}{d\delta} = \frac{u - \frac{vx}{\sqrt{x^2 + \delta^2}}}{-\frac{v \delta}{\sqrt{x^2 + \delta^2}}} = \frac{u\sqrt{x^2 + \delta^2} - vx}{-v \delta} = \frac{vx - u\sqrt{x^2 + \delta^2}}{v \delta}. vδdxdδ=vx−ux2+δ2v \delta \frac{dx}{d\delta} = vx - u\sqrt{x^2 + \delta^2}.

Let x=δf(δ)x = \delta f(\delta). vδ(f+δf′)=vδf−uδ2f2+δ2=vδf−uδf2+1v \delta (f + \delta f') = v \delta f - u \sqrt{\delta^2 f^2 + \delta^2} = v \delta f - u \delta \sqrt{f^2 + 1}. vδ2f′=−uδf2+1v \delta^2 f' = -u \delta \sqrt{f^2 + 1}. vδf′=−uf2+1v \delta f' = -u \sqrt{f^2 + 1}. vδdfdδ=−uf2+1v \delta \frac{df}{d\delta} = -u \sqrt{f^2 + 1}. dff2+1=−uvdδδ\frac{df}{\sqrt{f^2 + 1}} = -\frac{u}{v} \frac{d\delta}{\delta}. Integrating both sides: ∫dff2+1=−uv∫dδδ\int \frac{df}{\sqrt{f^2 + 1}} = -\frac{u}{v} \int \frac{d\delta}{\delta}. arsinh(f)=−uvln⁡δ+C\text{arsinh}(f) = -\frac{u}{v} \ln \delta + C. arsinh(xδ)=−uvln⁡δ+C\text{arsinh}(\frac{x}{\delta}) = -\frac{u}{v} \ln \delta + C.

At t=0t=0, y=0y=0, so δ=b−0=b\delta = b-0 = b. Also x=0x=0. arsinh(0b)=−uvln⁡b+C\text{arsinh}(\frac{0}{b}) = -\frac{u}{v} \ln b + C. arsinh(0)=0\text{arsinh}(0) = 0, so C=uvln⁡bC = \frac{u}{v} \ln b. arsinh(xb−y)=−uvln⁡(b−y)+uvln⁡b=uvln⁡(bb−y)\text{arsinh}(\frac{x}{b-y}) = -\frac{u}{v} \ln (b-y) + \frac{u}{v} \ln b = \frac{u}{v} \ln \left(\frac{b}{b-y}\right). xb−y=sinh⁡(uvln⁡(bb−y))\frac{x}{b-y} = \sinh \left(\frac{u}{v} \ln \left(\frac{b}{b-y}\right)\right).

Now consider the time. dydt=v(b−y)x2+(b−y)2=v(b−y)(b−y)2sinh⁡2(uvln⁡bb−y)+(b−y)2\frac{dy}{dt} = \frac{v(b-y)}{\sqrt{x^2 + (b-y)^2}} = \frac{v(b-y)}{\sqrt{(b-y)^2 \sinh^2 \left(\frac{u}{v} \ln \frac{b}{b-y}\right) + (b-y)^2}}. dydt=v(b−y)(b−y)sinh⁡2(uvln⁡bb−y)+1=vcosh⁡2(uvln⁡bb−y)=vcosh⁡(uvln⁡bb−y)\frac{dy}{dt} = \frac{v(b-y)}{(b-y) \sqrt{\sinh^2 \left(\frac{u}{v} \ln \frac{b}{b-y}\right) + 1}} = \frac{v}{\sqrt{\cosh^2 \left(\frac{u}{v} \ln \frac{b}{b-y}\right)}} = \frac{v}{\cosh \left(\frac{u}{v} \ln \frac{b}{b-y}\right)}. dtdy=1vcosh⁡(uvln⁡bb−y)\frac{dt}{dy} = \frac{1}{v} \cosh \left(\frac{u}{v} \ln \frac{b}{b-y}\right). Let z=uvln⁡bb−yz = \frac{u}{v} \ln \frac{b}{b-y}. dzdy=uvb−ybb(b−y)2=uv(b−y)\frac{dz}{dy} = \frac{u}{v} \frac{b-y}{b} \frac{b}{(b-y)^2} = \frac{u}{v(b-y)}. dy=v(b−y)udzdy = \frac{v(b-y)}{u} dz. dtdz=dtdydydz=1vcosh⁡(z)⋅v(b−y)u=b−yucosh⁡(z)\frac{dt}{dz} = \frac{dt}{dy} \frac{dy}{dz} = \frac{1}{v} \cosh(z) \cdot \frac{v(b-y)}{u} = \frac{b-y}{u} \cosh(z). Since z=uvln⁡bb−yz = \frac{u}{v} \ln \frac{b}{b-y}, ln⁡bb−y=vzu\ln \frac{b}{b-y} = \frac{vz}{u}, bb−y=evz/u\frac{b}{b-y} = e^{vz/u}, b−y=be−vz/ub-y = b e^{-vz/u}. dtdz=be−vz/uucosh⁡(z)=bue−vz/uez+e−z2=b2u(ez(1−v/u)+e−z(1+v/u))\frac{dt}{dz} = \frac{b e^{-vz/u}}{u} \cosh(z) = \frac{b}{u} e^{-vz/u} \frac{e^z + e^{-z}}{2} = \frac{b}{2u} (e^{z(1-v/u)} + e^{-z(1+v/u)}).

We need to integrate from y=0 to y=b. When y=0, z=uvln⁡bb=0z = \frac{u}{v} \ln \frac{b}{b} = 0. When y=b, ln⁡b0\ln \frac{b}{0} is undefined. This approach seems problematic.

Let's consider the time taken to cross the channel in the y-direction. dt=dyvy=x2+(b−y)2v(b−y)dydt = \frac{dy}{v_y} = \frac{\sqrt{x^2 + (b-y)^2}}{v(b-y)} dy. Let b−y=δb-y = \delta. dy=−dδdy = -d\delta. T=∫b0x2+δ2vδ(−dδ)=∫0bx2+δ2vδdδT = \int_b^0 \frac{\sqrt{x^2 + \delta^2}}{v \delta} (-d\delta) = \int_0^b \frac{\sqrt{x^2 + \delta^2}}{v \delta} d\delta. We know xδ=sinh⁡(uvln⁡bδ)\frac{x}{\delta} = \sinh \left(\frac{u}{v} \ln \frac{b}{\delta}\right). x=δsinh⁡(uvln⁡bδ)x = \delta \sinh \left(\frac{u}{v} \ln \frac{b}{\delta}\right). x2+δ2=δ2sinh⁡2(uvln⁡bδ)+δ2=δsinh⁡2(uvln⁡bδ)+1=δcosh⁡(uvln⁡bδ)\sqrt{x^2 + \delta^2} = \sqrt{\delta^2 \sinh^2 \left(\frac{u}{v} \ln \frac{b}{\delta}\right) + \delta^2} = \delta \sqrt{\sinh^2 \left(\frac{u}{v} \ln \frac{b}{\delta}\right) + 1} = \delta \cosh \left(\frac{u}{v} \ln \frac{b}{\delta}\right). T=∫0bδcosh⁡(uvln⁡bδ)vδdδ=1v∫0bcosh⁡(uvln⁡bδ)dδT = \int_0^b \frac{\delta \cosh \left(\frac{u}{v} \ln \frac{b}{\delta}\right)}{v \delta} d\delta = \frac{1}{v} \int_0^b \cosh \left(\frac{u}{v} \ln \frac{b}{\delta}\right) d\delta. Let w=ln⁡bδw = \ln \frac{b}{\delta}. When δ→0\delta \to 0, w→∞w \to \infty. When δ=b\delta = b, w=ln⁡1=0w = \ln 1 = 0. bδ=ew\frac{b}{\delta} = e^w, δ=be−w\delta = b e^{-w}. dδ=−be−wdwd\delta = -b e^{-w} dw. T=1v∫∞0cosh⁡(uvw)(−be−w)dw=bv∫0∞cosh⁡(uvw)e−wdwT = \frac{1}{v} \int_\infty^0 \cosh \left(\frac{u}{v} w\right) (-b e^{-w}) dw = \frac{b}{v} \int_0^\infty \cosh \left(\frac{u}{v} w\right) e^{-w} dw. T=bv∫0∞euw/v+e−uw/v2e−wdw=b2v∫0∞(e(u/v−1)w+e−(u/v+1)w)dwT = \frac{b}{v} \int_0^\infty \frac{e^{uw/v} + e^{-uw/v}}{2} e^{-w} dw = \frac{b}{2v} \int_0^\infty (e^{(u/v - 1)w} + e^{-(u/v + 1)w}) dw. T=b2v[e(u/v−1)wu/v−1−e−(u/v+1)wu/v+1]0∞T = \frac{b}{2v} \left[ \frac{e^{(u/v - 1)w}}{u/v - 1} - \frac{e^{-(u/v + 1)w}}{u/v + 1} \right]_0^\infty. For the upper limit at w=∞w=\infty, we need the exponents to be negative. u/v−1<0  ⟹  u<vu/v - 1 < 0 \implies u < v. −(u/v+1)<0-(u/v + 1) < 0 is always true since u, v > 0. So, we must have u<vu < v. Assuming this, the terms at w=∞w=\infty are 0. At w=0w=0, e0=1e^0 = 1. T=b2v[(0−0)−(1u/v−1−1u/v+1)]T = \frac{b}{2v} \left[ (0 - 0) - \left( \frac{1}{u/v - 1} - \frac{1}{u/v + 1} \right) \right]. T=−b2v(vu−v−vu+v)=−b2(1u−v−1u+v)T = -\frac{b}{2v} \left( \frac{v}{u - v} - \frac{v}{u + v} \right) = -\frac{b}{2} \left( \frac{1}{u - v} - \frac{1}{u + v} \right). T=−b2(u+v−(u−v)(u−v)(u+v))=−b2(2vu2−v2)=−bvu2−v2=bvv2−u2T = -\frac{b}{2} \left( \frac{u + v - (u - v)}{(u - v)(u + v)} \right) = -\frac{b}{2} \left( \frac{2v}{u^2 - v^2} \right) = -\frac{bv}{u^2 - v^2} = \frac{bv}{v^2 - u^2}.

This matches option (A). The condition v > u is necessary for the integral to converge at the upper limit, and also physically, if u >= v, the boat would be swept downstream faster than it can make progress across, and might not reach the dock at (0,b) if the river is infinitely long. However, the question asks for the time taken to reach the dock, implying it is reachable.