Question

Suppose U = { 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 } , A = { 3, 4, 5, 6, 9 } , B = { 3, 7, 9, 5 } and C =
{ 6, 8, 10, 12, 7 }. Write down the following set and draw Venn diagram for : A’

Answer 1

Hint:- In this question first of all we have to assume that set U is a universal set in which both set A and set B are inscribed. And as we all know that if P is a universal set and set X is inscribed in P then X’ must be set P – set X.

Complete step-by-step answer:
Now let us assume U as a universal set.
So, U = { 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 }
And A = { 3, 4, 5, 6, 9 } , B = { 3, 7, 9, 5 } and C = { 6, 8, 10, 12, 7 }
Now as we all know that
A’ must be equal to the universal set – set A.
So, A’ = U – A or we can say that A’ must have all the other values of other sets that are inscribed in universal set U apart from set A.
Now the diagram given below will describe the set U, set A , set B and set C.

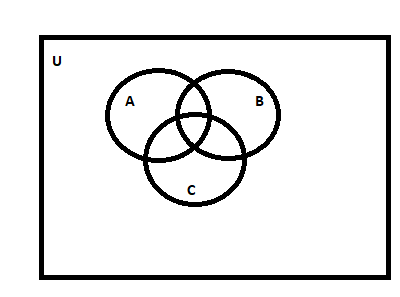
This diagram represents that sets A , B, C all are in the universal set U.
Now set A = { 3, 4, 5, 6, 9 } so set A’ = { 7, 8, 10, 11, 12 , 13 } which must be equal to all the values apart from set A.
Now let us highlight the A’ region in the Venn diagram by shading .
So, the diagram given below shows us the value or we can say the region of A’ .

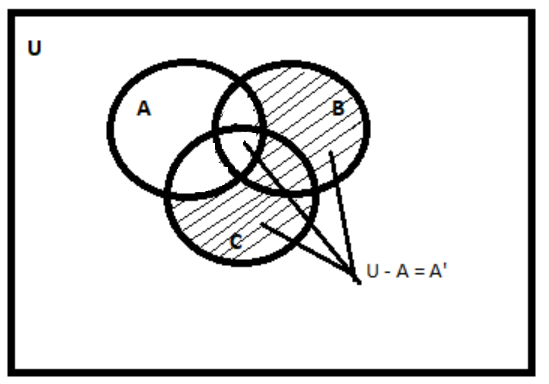
Note:- Whenever we come up with this type of problem then always we have to keep in mind that the complement of any set here ( A’ ) is counted as a subtraction of the universal set and the set whose complement is asked in the question. The complement can also have the values such as $A \cap B$, $B \cap C$,$C \cap A$ and $A \cap B \cap C$ from the set but the only set A portion must not be included.