Question

Suppose there are two windows in a house. A window of the house is at a height of $1.5m$ above the ground and the other window is $3m$ vertically above the lower window. Anil and Sanjeev are sitting inside the two windows. At an instant, the angles of elevation of a balloon from these windows are observed as $45^\circ$ and $30^\circ$ respectively. Find the height of the balloon from the ground.

Answer 1

In this question, we have been asked to find the height of the balloon from the ground. We have been given the angles of elevation from the two different windows and the height of the windows from the ground. First, draw the figure as described in the question. Then, use $\tan 45^\circ$ to find the relation between two sides. Now, use another triangle with $\tan 30^\circ$ to find the relation between the two sides. Use both the equations and the given distances to find the height of the balloon.

Complete step-by-step solution:
We have been told that two boys from different windows and different angles saw a balloon. And we have been asked to find the height of the balloon from the ground. We have been given the height of the window and the angles at which the balloon was seen.
Let us make the figure first.

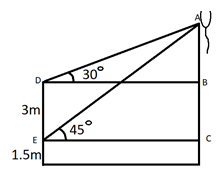
Balloon has been shown at the point A. Anil saw the balloon from the point E whereas Sanjeev saw the balloon from the point D. We can infer from the figure that $BD = EC$ and $DE = BC = 3m$. We have to find the length AC.
In the $\vartriangle AEC$, $\angle AEC = 45^\circ$. We can write,
$\Rightarrow \tan 45^\circ = \dfrac{{AC}}{{EC}}$
We know that $\tan 45^\circ = 1$,
$\Rightarrow 1 = \dfrac{{AC}}{{EC}}$
We can write $AC = AB + BC$ and we can see that $BC = 3m$. $\Rightarrow AC = AB + 3$. Putting in the above equation,
$\Rightarrow EC = AB + 3$ …. (1)
In $\vartriangle ABD,\angle ADB = 30^\circ$. We can write,
$\Rightarrow \tan 30^\circ = \dfrac{{AB}}{{BD}}$
We know, $BD = EC$.
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{AB}}{{EC}}$
On shifting we will have,
$\Rightarrow EC = AB\sqrt 3$ …. (2)
We will put this in equation (1),
$\Rightarrow AB + 3 = AB\sqrt 3$
Shifting to find the value of AB,
$\Rightarrow AB\sqrt 3 - AB = 3$
$\Rightarrow AB\left( {\sqrt 3 - 1} \right) = 3$
$\Rightarrow AB = \dfrac{3}{{\sqrt 3 - 1}}$
We will rationalise the RHS of the equation,
$\Rightarrow AB = \dfrac{3}{{\sqrt 3 - 1}} \times \dfrac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}}$
$\Rightarrow AB = \dfrac{{3\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} = \dfrac{{3\left( {\sqrt 3 + 1} \right)}}{2}$
Now, we have the value of AB. The height of the balloon from the ground = $AB + BC + 1.5$
$\Rightarrow \dfrac{{3\left( {\sqrt 3 + 1} \right)}}{2} + 3 + 1.5$
On solving,
$\Rightarrow \left( {1.5\sqrt 3 + 6} \right)m$

$\therefore$ The height of the balloon from the ground is $\left( {1.5\sqrt 3 + 6} \right)m$.

Note: If a person stands and looks up at an object, the angle of elevation is the angle between the horizontal line of sight and the object. If a person stands and looks down at an object, the angle of depression is the angle between the horizontal line of sight and the object.