Question

Suppose, there are two windows in a house. A window of the house is at a height of $1.5{\rm{m}}$ above the ground and the other window is $3{\rm{m}}$ vertically above the lower window. Anil and Sanjeev are sitting inside the two windows. At an instant, the angles of elevation of a balloon from these windows are observed as $45^\circ$ and $30^\circ$, respectively.
Find the height of the balloon from the ground.

Answer 1

Here, we will draw a figure depicting the given information and then we will use the properties of trigonometric functions in a triangle to find two different equations. Solving these equations, we will get a part of the required height of the balloon from the ground which when substituted to the total required height, will give us the required height of the balloon from the ground.

Formula Used:
$\tan \theta = \dfrac{P}{B}$, where $P$ is the perpendicular side and $B$ is the base of the triangle

Complete step-by-step answer:
According to the question, there are two windows in a house.
Let the lower window be at point $E$ which is $1.5{\rm{m}}$ above the ground and the other window be at point $D$ which is $3{\rm{m}}$ vertically above the lower window.
Let Anil be sitting at the lower window, his angle of elevation of the balloon present at point $A$ is given as $45^\circ$.
Let Sanjeev be sitting at the upper window, his angle of elevation of the balloon present at point $A$is given as $30^\circ$
Hence, we will draw a figure showing the above information as:

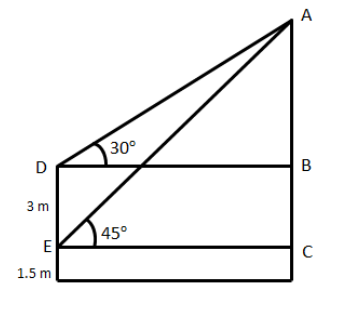
Now, from the figure, we can see
$DE = BC = 3{\rm{m}}$
$DB = EC$
Hence, $BCED$ is forming a rectangle.
Now, in the right triangle $AEC$ using the formula $\tan \theta = \dfrac{P}{B}$, we get
$\tan 45^\circ = \dfrac{{AC}}{{EC}}$
By using $\tan 45^\circ = 1$, we get
$\Rightarrow 1 = \dfrac{{AC}}{{EC}}$
On cross multiplication, we get
$\Rightarrow AC = EC$…………………………………..$\left( 1 \right)$
But, from the figure, $AC = AB + BC$ and $BC = 3{\rm{m}}$. Hence,
$AC = AB + 3$
Substituting $AC = AB + 3$ in equation $\left( 1 \right)$, we get,
$\Rightarrow AB + 3 = EC$…………………………….$\left( 2 \right)$
Now, in triangle $ADB$, using the formula $\tan \theta = \dfrac{P}{B}$, we get
$\tan 30^\circ = \dfrac{{AB}}{{BD}}$
Substituting $DB = EC$ and $\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$ in the above equation, we get
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{AB}}{{EC}}$
Substituting $EC = AB + 3$ from equation $\left( 2 \right)$, we get
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{AB}}{{AB + 3}}$
On cross multiplying, we get
$\Rightarrow \sqrt 3 AB = AB + 3$
$\Rightarrow \left( {\sqrt 3 - 1} \right)AB = 3$
Dividing both sides by $\left( {\sqrt 3 - 1} \right)$, we get
$\Rightarrow AB = \dfrac{3}{{\left( {\sqrt 3 - 1} \right)}}$
Now, rationalizing the RHS, we get
$\Rightarrow AB = \dfrac{3}{{\left( {\sqrt 3 - 1} \right)}} \times \dfrac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}}$
Using the formula, $\left( {a - b} \right)\left( {a + b} \right) = {a^2} - {b^2}$ in the denominator
$\Rightarrow AB = \dfrac{{3\left( {\sqrt 3 + 1} \right)}}{{{{\left( {\sqrt 3 } \right)}^2} - 1}}$
Simplifying the expression, we get
$\Rightarrow AB = \dfrac{{3\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} = \dfrac{{3\left( {\sqrt 3 + 1} \right)}}{2}$
Now, we are having the value of $AB$ and using this we will find the height of the balloon from the ground.
Height of the balloon from the ground $= 1.5 + BC + AB$
Substituting $BC = 3{\rm{m}}$ and $AB = \dfrac{{3\left( {\sqrt 3 + 1} \right)}}{2}$ in the above equation, we get
$\Rightarrow$ Height of the balloon from the ground $= 1.5 + 3 + \dfrac{{3\left( {\sqrt 3 + 1} \right)}}{2}$
Simplifying the expression, we get
$\Rightarrow$ Height of the balloon from the ground $= 4.5 + \dfrac{{3\sqrt 3 + 3}}{2}$
Taking the LCM and simplifying the expression, we get,
$\Rightarrow$ Height of the balloon from the ground $= \dfrac{{9 + 3\sqrt 3 + 3}}{2}$
Adding the like terms, we get
$\Rightarrow$ Height of the balloon from the ground $= \dfrac{{12 + 3\sqrt 3 }}{2}$
Dividing the numerator by 2, we get
$\Rightarrow$ Height of the balloon from the ground $= \left( {6 + 1.5\sqrt 3 } \right){\rm{m}}$
We know that $\sqrt 3 = 1.732$.Hence,
$\Rightarrow$ Height of the balloon from the ground $= \left( {6 + 1.5 \times 1.732} \right)$
Simplifying the expression, we get
$\Rightarrow$ Height of the balloon from the ground $= 8.598 \approx 8.6{\rm{m}}$
Therefore, the required height of the balloon from the ground is $\left( {6 + 1.5\sqrt 3 } \right){\rm{m}}$or $8.6{\rm{m}}$ (approx.)
Hence, this is the required answer.

Note: In the applications of trigonometry, to show the angle of elevation, we draw an imaginary line of sight which is always parallel to the base. The angle between that imaginary line of sight and the line joining the object is called the angle of elevation. The angle of elevation is always above the line of sight as it actually means ‘looking up’. Whereas, the angle of depression is always below the line of sight as in simple terms it means ‘looking down’. The angle of elevation and the angle of depression are actually congruent to each other.