Question

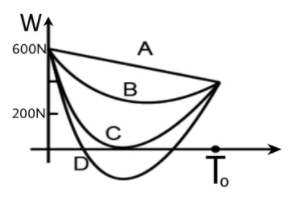
Suppose, the acceleration due to gravity at the Earth's surface is $10ms^{-2}$ and at the surface of Mars it is $4ms^{-2}$ . A 60 kg passenger goes from the Earth to Mars in a spaceship moving with a constant velocity. Neglect all other objects in the sky. Which part of the figure best represents the weight (net gravitational force) of the passenger as a function of time?

Answer 1

Now in order to solve this question we must take in mind that the force of gravity according to Newton's law is inversely proportional to the square of the distance between the object. Since both earth and mars are attracting the same object there also comes a time when the forces of gravitation are balanced.

Complete answer:
Since the force of gravitation is inversely proportional to the square of the distance between them the net resultant graphs are never going to be a straight line it will always be a curved line.
Thus, we can now eliminate the option (A)
Now the mass of the person is 60 kgs so it's weight will be 600N thus the graph will start from 600N. It's weight on Mars will be 400N so the graph will end at 400N.
Now there will be a time when the force of attraction from earth will be exactly equal to that of the force of attraction from Mars. But they will be in the opposite direction with each other. So, they will cancel each other out. At this point the net force on the Person will be zero so there will be a time when it's weight will be zero which is only shown in the graph (C)

So, the correct option is (C).

Note:
The person in this question is stuck between two planets which are earth and Mars. If it is not stuck in between then and is moving away from both of them then he will be acted upon by the force of attraction from both the planets but in this case the forces will never cancel out each other. Thus, he will never experience a net weight of zero Newton. And options (B) can be considered as an answer.