Question

Suppose that Young's double slit experiment is carried out with sodium (Yellow) light of wavelength $589.3nm$ and the interference pattern is observed on a $100cm$ away. The ${{10}^{th}}$ bright fringe has its centre at a distance of $12mm$ from the central maximum. Find out the separation between the slits.
$\begin{aligned} & A.0.49mm \\\ & B.0.06mm \\\ & C.0.7mm \\\ & D.0.53mm \\\ \end{aligned}$

Answer 1

The fringe width can be found by taking the ratio of the product of order of the fringe, the wavelength of the light used and the distance between the slit and source to the distance between the slits. From this find out the distance between the slits by rearranging the equation. This will help you in answering this question.

Complete step by step answer:

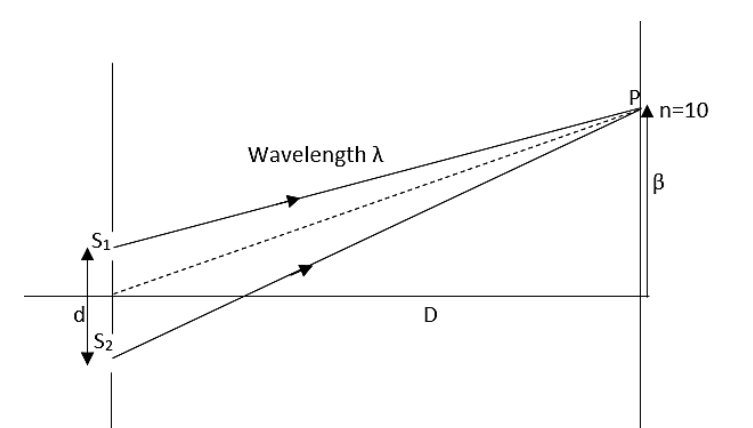
It has been mentioned in the question that the order of the bright fringe formed will be,
$n=10$
The wavelength of the light used can be written as,
$\lambda =589.3nm$
Fringe width from the central maximum can be written as,
$\beta =12mm$
The distance between the slit and source can be written as,
$D=100cm=1m$
As we all know, the fringe width can be found using the equation,
$\beta =\dfrac{n\lambda D}{d}$
Let us substitute this in the equation. That is we can write that,
$\Rightarrow 12\times {{10}^{-3}}=\dfrac{10\times 589.3\times {{10}^{-9}}\times 1}{d}$
Rearrange this equation in terms of the distance between the sits. That is,

&\Rightarrow d=\dfrac{10\times 589.3\times {{10}^{-9}}\times 1}{12\times {{10}^{-3}}} \\\ & \Rightarrow d=\dfrac{10\times 589.3\times {{10}^{-6}}}{12}=0.49mm \\\ & \Rightarrow d=0.49mm \\\ \end{aligned}$$ **So, the correct answer is “Option A”.** **Note:** Young's double slit experiment is a perfect representation of the dual characteristics of a particle in modern physics. It assures that the matter is having both the characteristics of particles as well as the wave. The distance between the consecutive bright and the dark fringes are termed as fringe width which will be equal in all the consecutive bright and the dark fringes in the young’s double slit experiment.