Solveeit Logo
Login

Question

Question: Suppose that on a two lane road, car A is travelling with a speed of \(36km{{h}^{-1}}\). This time t...

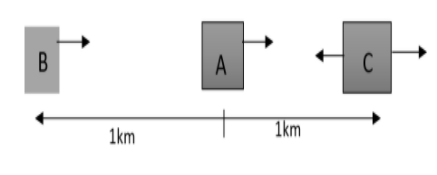
Suppose that on a two lane road, car A is travelling with a speed of 36kmh−136km{{h}^{-1}}. This time two cars B and C approach car A in the opposite directions with a speed of 54kmh−154km{{h}^{-1}}each. At a specific moment, if the distance AB is equal to AC, both being 1km1km, B decides to overtake A before C does. Calculate the minimum acceleration of car B is required to avoid an accident?

Explanation

Solution

Convert the velocities in terms of metre per second. Find the relative speed of the car A with respect to the car C. calculate the time taken by car C to overtake A. Then the distance travelled by the car A should be found. Use the third equation of motion finally to find the answer. This all will help you in answering this question.

Complete step by step answer:
The speed of the car A has been given as,
SA=36kmh−1=36×518=10ms−1{{S}_{A}}=36km{{h}^{-1}}=36\times \dfrac{5}{18}=10m{{s}^{-1}}
The speed of the car B and car C has been given as,
SB=SC=54kmh−1=54×518=15ms−1{{S}_{B}}={{S}_{C}}=54km{{h}^{-1}}=54\times \dfrac{5}{18}=15m{{s}^{-1}}
The relative speed of A with respect to C will be,
SAC=SC+SA=10+15=25ms−1{{S}_{AC}}={{S}_{C}}+{{S}_{A}}=10+15=25m{{s}^{-1}}
Therefore the time taken by C in order to overtake A is given as,
t=100025=40st=\dfrac{1000}{25}=40s
The distance travelled by A all this time can be found as,
dA=10×40=400m{{d}_{A}}=10\times 40=400m
From this we can understand that car B has to travel a distance which is the sum of the distances covered by A and C.
dA=400m dC=1km=1000m \begin{aligned} & {{d}_{A}}=400m \\\ & {{d}_{C}}=1km=1000m \\\ \end{aligned}
That is,
dB=1000+400=1400m{{d}_{B}}=1000+400=1400m
That is 1400m1400m to take over A before C has been done in 40s40s. Apply this in the equation of motion,
s=ut+12at2s=ut+\dfrac{1}{2}a{{t}^{2}}
Substituting the values in it will give,
1400=15×40+12a×(40)2 ⇒800=a×800 \begin{aligned} & 1400=15\times 40+\dfrac{1}{2}a\times {{\left( 40 \right)}^{2}} \\\ & \Rightarrow 800=a\times 800 \\\ \end{aligned}
Rearranging the equation gives,
a=1ms−2a=1m{{s}^{-2}}

Note: The velocity is the time rate of variation of the displacement. Distance covered is the total length of the path traversed by a body. The displacement is the shortest distance between the initial and final points. Time rate of variation of distance is known as speed. Acceleration is the time rate of variation of velocity.