Question

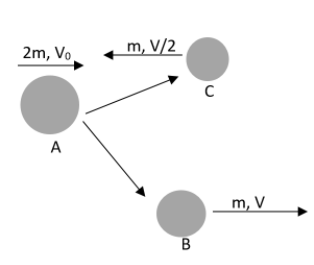
Suppose that a nucleus A, having a specific de - Broglie wavelength ${{\lambda }_{A}}$gets divided into two nuclei B and C of equal mass because of the spontaneous fission. At this situation, B flies in the identical direction as that of A. But C flies in the direction opposite to this with a velocity equivalent to half of that of B. calculate the de Broglie wavelengths ${{\lambda }_{B}}$​ and ${{\lambda }_{C}}$​ of B and C?
$\begin{aligned} & A.2{{\lambda }_{A}},{{\lambda }_{A}} \\\ & B.{{\lambda }_{A}},2{{\lambda }_{A}} \\\ & C.{{\lambda }_{A}},\dfrac{{{\lambda }_{A}}}{2} \\\ & D.\dfrac{{{\lambda }_{A}}}{2},{{\lambda }_{A}} \\\ \end{aligned}$

Answer 1

Apply the conservation of momentum at first as per the mentioning in the question. Then find out the velocity of A. Using these values, find out the de Broglie wavelength which will be the ratio of the Planck’s constant to the momentum of the body. This will help you in answering this question.

Complete step by step answer:
It has been mentioned in the question that the mass of the nuclei, B and C are equal. Therefore let us assume that the mass of both the bodies is $m$. And also it has been mentioned that the velocity of C is half of that of B and they are moving in opposite directions. Therefore we can write that,
${{V}_{C}}=-\dfrac{{{V}_{B}}}{2}$
And the velocity of B is in the same direction of A also. We can apply the momentum conservation here. It can be written as,
$2m{{V}_{A}}=mV-m\dfrac{V}{2}$
Simplifying this equation will give the value of the velocity of the nucleus A.
That is,
$V=4{{V}_{A}}$
The momentum corresponding to each of the nuclei can be written as,
$\begin{aligned} & {{P}_{A}}=2m{{V}_{0}} \\\ & {{P}_{B}}=4m{{V}_{0}} \\\ & {{P}_{C}}=2m{{V}_{0}} \\\ \end{aligned}$
Therefore the de Broglie wavelength can be written as,
$\lambda =\dfrac{h}{P}$
Where $h$ be the Planck’s constant.
Hence the de Broglie wavelength of each of the nuclei will be,
$\begin{aligned} & {{\lambda }_{A}}=\dfrac{h}{2m{{V}_{0}}} \\\ & {{\lambda }_{B}}=\dfrac{h}{4m{{V}_{0}}} \\\ & {{\lambda }_{C}}=\dfrac{h}{2m{{V}_{0}}} \\\ \end{aligned}$
Therefore the relation between wavelengths of B and C with respect to A will be,
$\begin{aligned} & {{\lambda }_{B}}=\dfrac{{{\lambda }_{A}}}{2} \\\ & {{\lambda }_{C}}={{\lambda }_{A}} \\\ \end{aligned}$
The answer is given as option D.

Note:
According to the dual nature of the wave, the De Broglie wavelength is a wavelength which can be related to all the bodies in quantum mechanics which represents the probability density of detecting the particle at a specific position of the configuration space.