Solveeit Logo
Login

Question

Question: Suppose \({T_1}\) is the time period of oscillation of a body suspended to a spring and \({T_2}\) is...

Suppose T1{T_1} is the time period of oscillation of a body suspended to a spring and T2{T_2} is the time period of oscillation of the same body suspended to another spring. If same body suspended to series combination of same two springs, what is its time period of oscillation ??
A. T1+T2{T_1} + {T_2}
B. T1T2T1+T2\dfrac{{{T_1}{T_2}}}{{{T_1} + {T_2}}}
C. T1T2T12+T22\dfrac{{{T_1}{T_2}}}{{\sqrt {T_1^2 + T_2^2} }}
D. T12+T22\sqrt {T_1^2 + T_2^2}

Explanation

Solution

In this question, we use the concept of series combination of springs when the body is suspended to it and oscillates. If two springs of spring constants k1{k_1} and k2{k_2} are joined in series, the resultant spring constant of the combination is given by
1ks=1k1+1k2\dfrac{1}{{{k_s}}} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}}

Formula used:
Time period of oscillation of a body attached to spring is given by
T=2πmkT = 2\pi \sqrt {\dfrac{m}{k}}
Where, mm - mass of the body / inertia factor and kk - spring constant of the spring.

Complete step by step answer:
Let us denote some terms to the given data for better understanding.
T1{T_1} - time period of oscillation of a body attached to the spring of constant k1{k_1}
T2{T_2} - time period of oscillation of a body attached to the spring of constant k2{k_2}
Writing the time period of oscillation for both springs,
T1=2πmk1−−−−−−−−−−−−−(1){T_1} = 2\pi \sqrt {\dfrac{m}{{{k_1}}}} - - - - - - - - - - - - - (1)
⇒T2=2πmk2−−−−−−−−−−−−−(2)\Rightarrow {T_2} = 2\pi \sqrt {\dfrac{m}{{{k_2}}}} - - - - - - - - - - - - - (2)
⇒T=2πmks−−−−−−−−−−−−−(3)\Rightarrow T = 2\pi \sqrt {\dfrac{m}{{{k_s}}}} - - - - - - - - - - - - - (3)
We have to calculate the combined period of oscillation when the body is attached to series combination of two springs as shown.

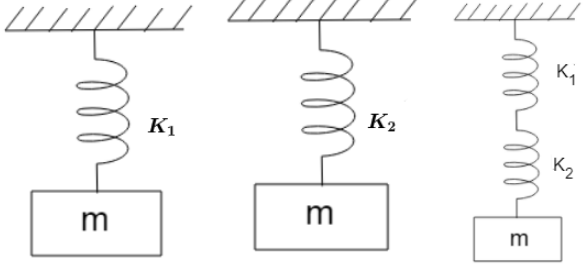
For series combination of springs, we have
1ks=1k1+1k2\dfrac{1}{{{k_s}}} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}}
⇒ks=k1k2k1+k2−−−−−−−−−−−(4)\Rightarrow {k_s} = \dfrac{{{k_1}{k_2}}}{{{k_1} + {k_2}}} - - - - - - - - - - - (4)
Now, squaring eq(1)(1) and eq(2)(2) and adding, we get
T12+T22=(2π)2(mk1+mk2)T_1^2 + T_2^2 = {\left( {2\pi } \right)^2}\left( {\dfrac{m}{{{k_1}}} + \dfrac{m}{{{k_2}}}} \right)
⇒T12+T22=(2π)2(m(k1+k2)k1k2)\Rightarrow T_1^2 + T_2^2 = {\left( {2\pi } \right)^2}\left( {\dfrac{{m({k_1} + {k_2})}}{{{k_1}{k_2}}}} \right)
⇒T12+T22=(2π)2(mks)−−−−−−−−−−\Rightarrow T_1^2 + T_2^2 = {\left( {2\pi } \right)^2}\left( {\dfrac{m}{{{k_s}}}} \right) - - - - - - - - - - From eq(4)(4)
⇒T12+T22=T2−−−−−−−−−−\Rightarrow T_1^2 + T_2^2 = {T^2} - - - - - - - - - - From eq (3)(3)
∴T=T12+T22\therefore T = \sqrt {T_1^2 + T_2^2}
The combined time period of oscillation of the body attached to two springs is T=T12+T22T = \sqrt {T_1^2 + T_2^2} .

Hence, option D is correct.

Additional information: If two springs of spring constants k1{k_1} and k2{k_2} are joined in parallel, the resultant spring constant of the combination is given by
kp=k1+k2{k_p} = {k_1} + {k_2}

Note: In this question, the same mass is suspended to the combination of springs, and hence, there is no change in mass of the body. The change will occur only in the spring constant of combined springs. There are two types of springs : Light spring and heavy spring.So, always look at what has been given in the question.In general, light springs are used. But, if the spring has mass MM and a mass mm is suspended from it, then the time period is given by
T=2πMeffkT = 2\pi \sqrt {\dfrac{{{M_{eff}}}}{k}} , where Meff=m+M3{M_{eff}} = m + \dfrac{M}{3}.