Question

Suppose n be an integer greater than 1, let $a_n = \frac{1}{log_n 2002}$. Suppose b = $a_2 + a_3 + a_4 + a_5$ and c = $a_{10} + a_{11} + a_{12} + a_{13} + a_{14}$. Then (b - c) equals

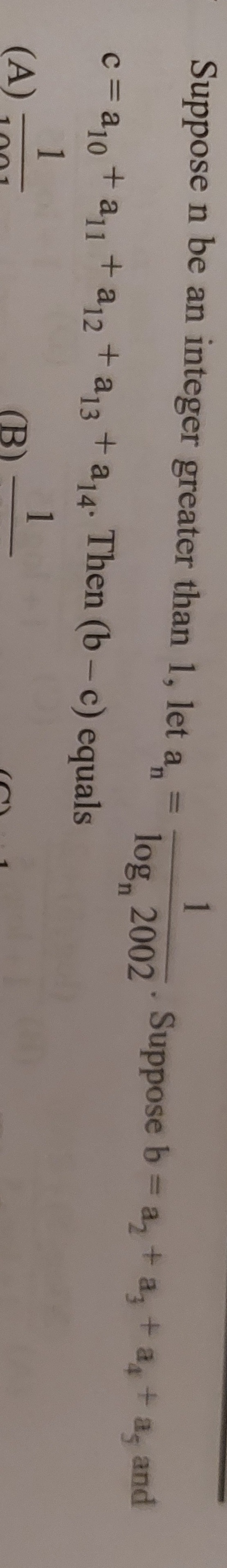
• A. $\frac{1}{1001}$
• B. 1

Answer 1

-1

Answer 2

1. Given

   $$a_n = \frac{1}{\log_n{2002}}.$$

   Use the change‐of-base formula:

   $$\log_n{2002} = \frac{\log{2002}}{\log{n}}\quad\Longrightarrow\quad a_n = \frac{\log{n}}{\log{2002}}.$$

2. Calculate $b$:

   $$b = a_2 + a_3 + a_4 + a_5 = \frac{\log2+\log3+\log4+\log5}{\log2002} = \frac{\log(2\cdot3\cdot4\cdot5)}{\log2002} = \frac{\log(120)}{\log2002}.$$

3. Calculate $c$:

   $$c = a_{10}+a_{11}+a_{12}+a_{13}+a_{14} = \frac{\log(10\cdot11\cdot12\cdot13\cdot14)}{\log2002} = \frac{\log(240240)}{\log2002}.$$

   Notice that

   $$10\cdot11\cdot12\cdot13\cdot14 = 120\cdot2002.$$

4. Find $b-c$:

   $$b-c = \frac{\log(120)-\log(240240)}{\log2002} = \frac{\log\left(\frac{120}{120\cdot2002}\right)}{\log2002} = \frac{\log\left(\frac{1}{2002}\right)}{\log2002}.$$

   Using the logarithm property $\log\left(\frac{1}{2002}\right) = -\log(2002)$, we get

   $$b-c = \frac{-\log(2002)}{\log2002} = -1.$$