Question

Suppose in an exceedingly circular motion of a particle , the tangential acceleration of the particle is given by $at\Rightarrow 9m/{{s}^{2}}$. The radius of the circle is 4m. The particle was initially at rest . Find the time after which acceleration of the particle makes an angle of ${{45}^{\circ }}$ with the radial accelerations is –
A. $\dfrac{1}{3}s$
B. $\dfrac{2}{3}s$
C. $\dfrac{4}{3}s$
D. $1s$

Answer 1

We know that the radial acceleration is equal to the rate of change in velocity . The change which generates in speed during the non uniform circular motion known as tangential acceleration.

Complete step-by-step solution:
let's draw a diagram of this question to solve this question-

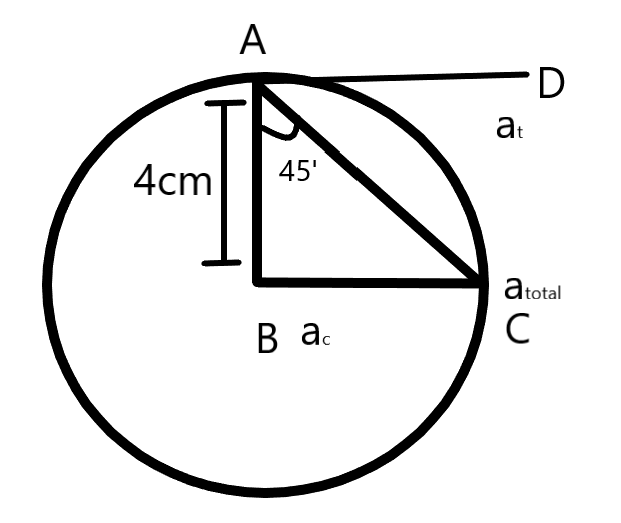
here in this problem , tangential acceleration = $9m/{{s}^{2}}$
Radius =$4m$
from the fig we get triangle ABC ,

& \tan {{45}^{\circ }}\Rightarrow \dfrac{at}{ac} \\\ & or,1\Rightarrow \dfrac{9}{ac} \\\ & or,ac\Rightarrow 9m/{{s}^{2}} \\\ \end{aligned}$$ Now , we know that tangential acceleration is $$at\Rightarrow \dfrac{dv}{dt}$$ $$or,dv\Rightarrow at.dt$$ $$or,\int_{0}^{v}{dv\Rightarrow \int\limits_{0}^{t}{9dt}}$$ $$or,v\Rightarrow 9t$$ $$m/s$$ Again , we know that centripetal acceleration $$\left( ac \right)=\dfrac{{{v}^{2}}}{r}$$ Now , using $$(ac)=(at)$$ we get $$\dfrac{{{v}^{2}}}{r}\Rightarrow \dfrac{dv}{dt}$$ $$or,\dfrac{{{(9t)}^{2}}}{4}\Rightarrow 9$$ $$or,\dfrac{81t}{4}\Rightarrow 9$$ $$or,{{1}^{2}}\Rightarrow \dfrac{4}{9}$$ $$or,t\Rightarrow \dfrac{2}{3}\sec $$ **Therefore, the correct option is B) $$\dfrac{2}{3}s$$.** **Note:** During circular motion the speed vector changes its direction at each point on the circle . This suggests that the tangential component of acceleration is always non-zero.