Question

Suppose a two dimensional rectangular material carries a current of $0.5A$ in the positive x-direction and is penetrated by a magnetic field of $1.4mT$ in the negative z-direction. The density of mobile charges per unit area of material is $0.2\mu C{m^{ - 2}}$ , what is the magnitude of the Hall voltage and the direction of the generated electric field? (Assume a right handed coordinate system)
(A) $70\mu V$ , negative y-direction
(B) $70\mu V$ , positive y-direction
(C) $3.5kV$ , negative y-direction
(D) $3.5kV$ , positive y-direction

Answer 1

Hint : Here, we have been asked about the Hall voltage and it is calculated by using the principle of Hall Effect. Hall Effect means when a conductor or semiconductor with current flowing in one direction was introduced perpendicular to a magnetic field a voltage could be measured at right angles to the current path. Let us apply this concept and find voltage.

Complete Step By Step Answer:
according to the given information we have
$I = 0.5A$ , $B = 1.4mT$ and $\dfrac{{Ne}}{A} = 0.2\mu C{m^{ - 2}}$
Formula for the Hall voltage is given by
${V_H} = \dfrac{{IB}}{{ned}}$ … $(1)$
Where,
$I$ is the current flowing through the conductor.
$B$ is the magnetic field of the conductor.
$e$ is the charge.
$n$ is the number of charge carriers per unit volume.
$d$ is the thickness of the conductor.
Also, we have to use $\dfrac{{Ne}}{A} = nde = 0.2\mu C{m^{ - 2}}$
In $eq(1)$ we have to put all the given data as follows:
$eq(1) \Rightarrow {V_H} = \dfrac{{(0.5)(1.4 \times {{10}^{ - 3}})}}{{(0.2 \times {{10}^{ - 6}})}}$
$\Rightarrow {V_H} = 3.5kV$
So, we have calculated the Hall voltage now we have to find the direction of the generated electric field.
Let us consider the right handed coordinate system as below:

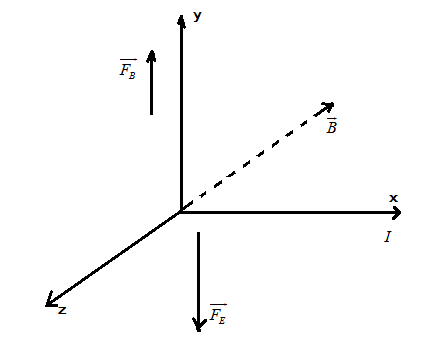
So, negative y-direction as ${I_B}$ and $\left( {\vec I \times \vec B} \right)l$ is in positive y-direction.
Thus, ${\vec F_E} = - {\vec F_B} =$ negative y-direction.
Thus, the answer is that the Hall voltage is $3.5kV$ and the electric field is in negative y-direction.

Note :
We must study the facts of Hall Effect and how it works to find hall voltage. We have to use the right handed coordinate system. Thus we have concluded above that the voltage is $3.5kV$ and the electric field is in negative y-direction.