Question

Suppose a parabola $y=a{{x}^{2}}+bx+c$ has two x intercepts one positive and one negative, and its vertex is (2,-2). Then which of the following is true?
(a) ab>0
(b) bc>0
(c) ca>0
(d) a+b+c>0

Answer 1

Hint: Vertex is at (2, -2) and the parabola cuts the x axis so it is an upward opening parabola. So we will use this information to draw the figure. And as the slope is zero we will get the relation between a and b by differentiating.

Complete step-by-step answer:
So it is mentioned in the question that the vertex is at (2, -2) and the parabola cuts the x axis once positive axis and once negative axis so it is an upward opening parabola.
So according to the details provided in the question the figure is:

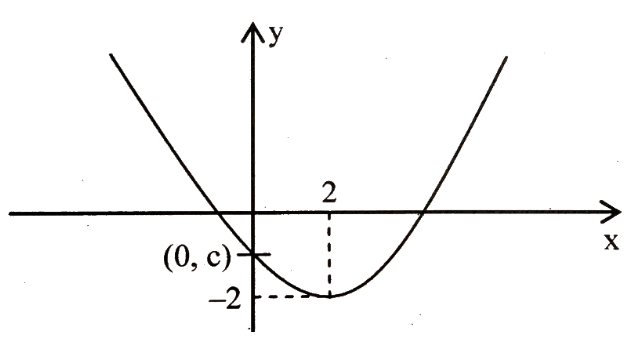
And we know that for an upward opening parabola a>0.
And at the vertex (2, -2) the slope is zero which means $\dfrac{dy}{dx}=0$. Hence using this information, we get,
$y=a{{x}^{2}}+bx+c.......(1)$
So differentiating equation (1) with respect to x we get,
$\dfrac{dy}{dx}=2ax+b.......(2)$
Now equating equation (2) with zero we get.,
$2ax+b=0.......(3)$
Now substituting 2 in place of x and solving for b we get,

& \Rightarrow 2a\times 2+b=0 \\\ & \Rightarrow b=-4a.........(4) \\\ \end{aligned}$$ Now we know that a>0 for upward parabola then from equation (4) we can clearly see that b<0\. And for such a parabola we can clearly see from the figure that the y intercept is positive. So here a>0, c<0 and from equation (4) b<0. So ab<0 as we are multiplying a positive quantity with negative quantity. So bc>0 as we are multiplying a negative quantity with negative quantity. And ca<0 as we are multiplying a positive quantity with negative quantity. And a+b+c<0 as both b and c are negative. So the right answer is option (b). Note: Drawing the figure is important as it makes everything clear. Also we need to remember that slope means differentiation of y with respect to x. We in a hurry can make a mistake in understanding the relation between a, b and c so we need to be careful while doing this step.