Question

summation r varies from 0 to (20+r C 10)(20-r C 10)

Answer 1

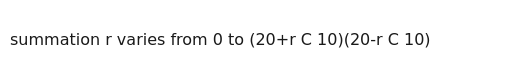
S=\frac{1}{2}\Biggl[\binom{41}{21}+\binom{20}{10}^2\Biggr]

Answer 2

We will show that

$$S=\sum_{r=0}^{20} \binom{20+r}{10}\binom{20-r}{10}$$

can be written in closed‐form. One very neat method is to “symmetrize” the sum. (Notice that although the original sum runs from $r=0$ to $20$, the summand is an even function of $r$ provided we extend $r$ to negative values.) In fact, one may prove (by a combinatorial argument or by generating functions) the following identity valid for nonnegative integers $n$ and $m$:

$$\sum_{r=-n}^{n}\binom{n+r}{m}\binom{n-r}{m}=\binom{2n+1}{2m+1}.$$

Now, in our case, take

$$n=20,\quad m=10.$$

Then

$$\sum_{r=-20}^{20}\binom{20+r}{10}\binom{20-r}{10}=\binom{41}{21}.$$

But observe that when we extend the sum to $r=-20$ to $20$ the summand is even. (A short check shows that replacing $r$ by $-r$ leaves $\binom{20+r}{10}\binom{20-r}{10}$ unchanged.) Hence the full sum satisfies

$$\sum_{r=-20}^{20}\binom{20+r}{10}\binom{20-r}{10} = \binom{20+0}{10}\binom{20-0}{10} + 2\sum_{r=1}^{20}\binom{20+r}{10}\binom{20-r}{10}.$$

That is,

$$\binom{41}{21} = \binom{20}{10}^2 + 2\sum_{r=1}^{20}\binom{20+r}{10}\binom{20-r}{10}.$$

But the sum we need is

$$S=\sum_{r=0}^{20}\binom{20+r}{10}\binom{20-r}{10} = \binom{20}{10}^2 + \sum_{r=1}^{20}\binom{20+r}{10}\binom{20-r}{10}.$$

So, solving for $S$ we obtain

$$2S - \binom{20}{10}^2=\binom{41}{21}\quad\Longrightarrow\quad S=\frac{1}{2}\Bigl[\binom{41}{21}+\binom{20}{10}^2\Bigr].$$

Thus, a correct answer is

$$\boxed{S=\frac{1}{2}\Biggl[\binom{41}{21}+\binom{20}{10}^2\Biggr]}.$$

---

Core Explanation:

1. Extend the sum from $r=0$ to $20$ to the symmetric sum from $r=-20$ to $20$.
2. Use the identity $\sum_{r=-n}^{n}\binom{n+r}{m}\binom{n-r}{m}=\binom{2n+1}{2m+1}$ with $n=20$ and $m=10$.
3. Since the summand is even, the full sum equals $\binom{20}{10}^2+2\sum_{r=1}^{20}\binom{20+r}{10}\binom{20-r}{10}$.
4. Solve for the original sum to get $S=\frac{1}{2}\left[\binom{41}{21}+\binom{20}{10}^2\right]$.

---

Answer:

$$\boxed{S=\frac{1}{2}\Biggl[\binom{41}{21}+\binom{20}{10}^2\Biggr]}$$

(No option number is needed since this is not a multiple‐choice problem.)

---

Additional details:

• Subject: Mathematics

• Chapter: Probability (as found in NCERT Class 12, which covers combinatorial ideas in Probability)

• Topic: Binomial Theorem and Binomial Coefficients

• Difficulty level: Hard

• Question type: descriptive

This approach is appropriate for a 12th grade student familiar with combinatorial identities and symmetry arguments.