Question
Question: $\sum_{R=1}^{7}\tan^{2}\frac{R\pi}{16}$...
∑R=17tan216Rπ
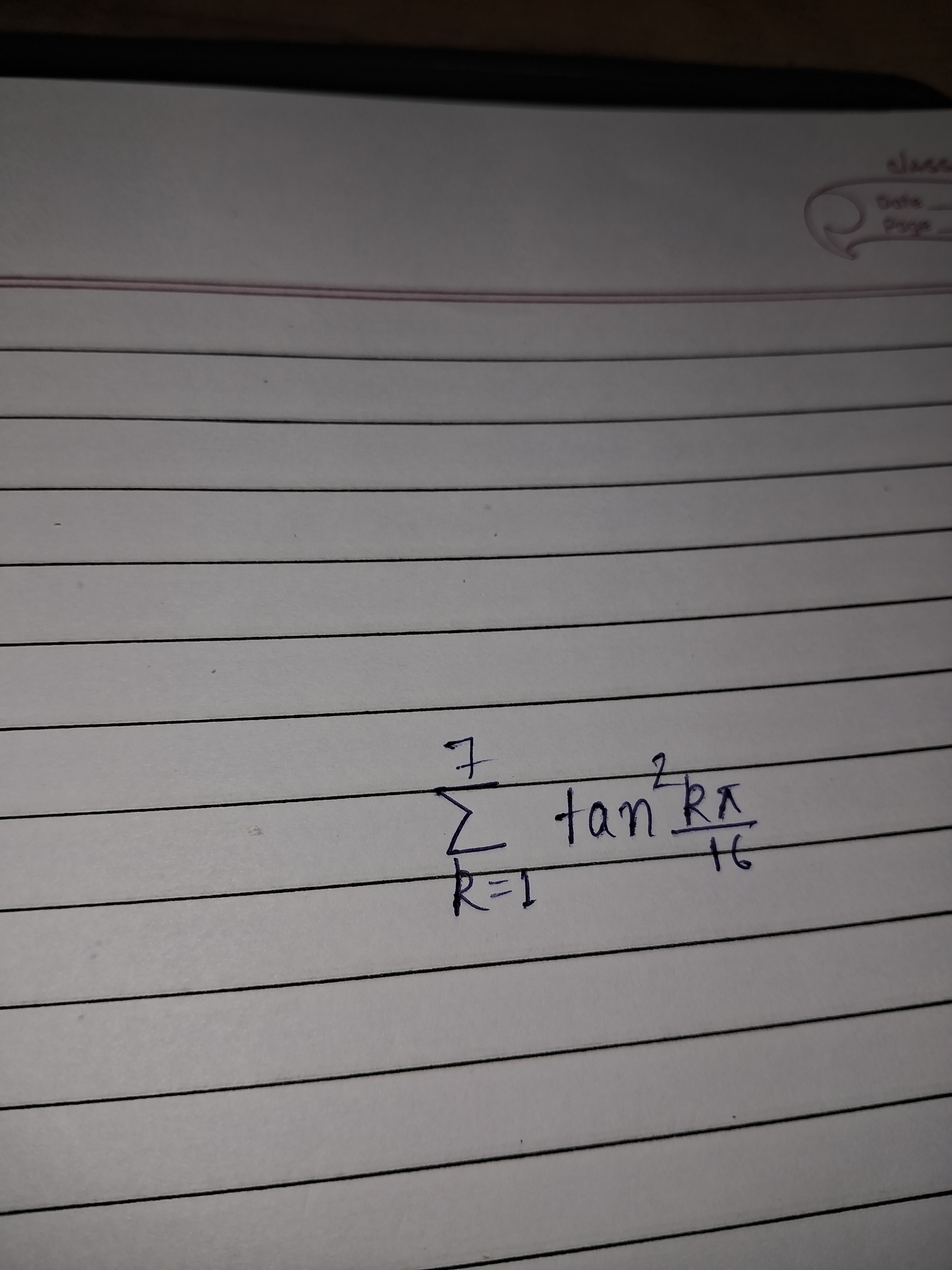
Answer
35
Explanation
Solution
The sum ∑R=17tan216Rπ is the sum of the roots of the polynomial in y=t2 derived from setting the numerator of tan(16x) to zero, where t=tanx. The polynomial is P(y)=(116)−(316)y+⋯−(1516)y7. The roots are tan2(16kπ) for k=1,…,7. By Vieta's formulas, the sum of these roots is −coeff of y7coeff of y6=−−(1516)(1316)=(116)(316)=16560=35.
