Solveeit Logo
Login

Question

Question: $\sum_{R=1}^{7} \tan^2\frac{R\pi}{16}$...

∑R=17tan⁡2Rπ16\sum_{R=1}^{7} \tan^2\frac{R\pi}{16}

A

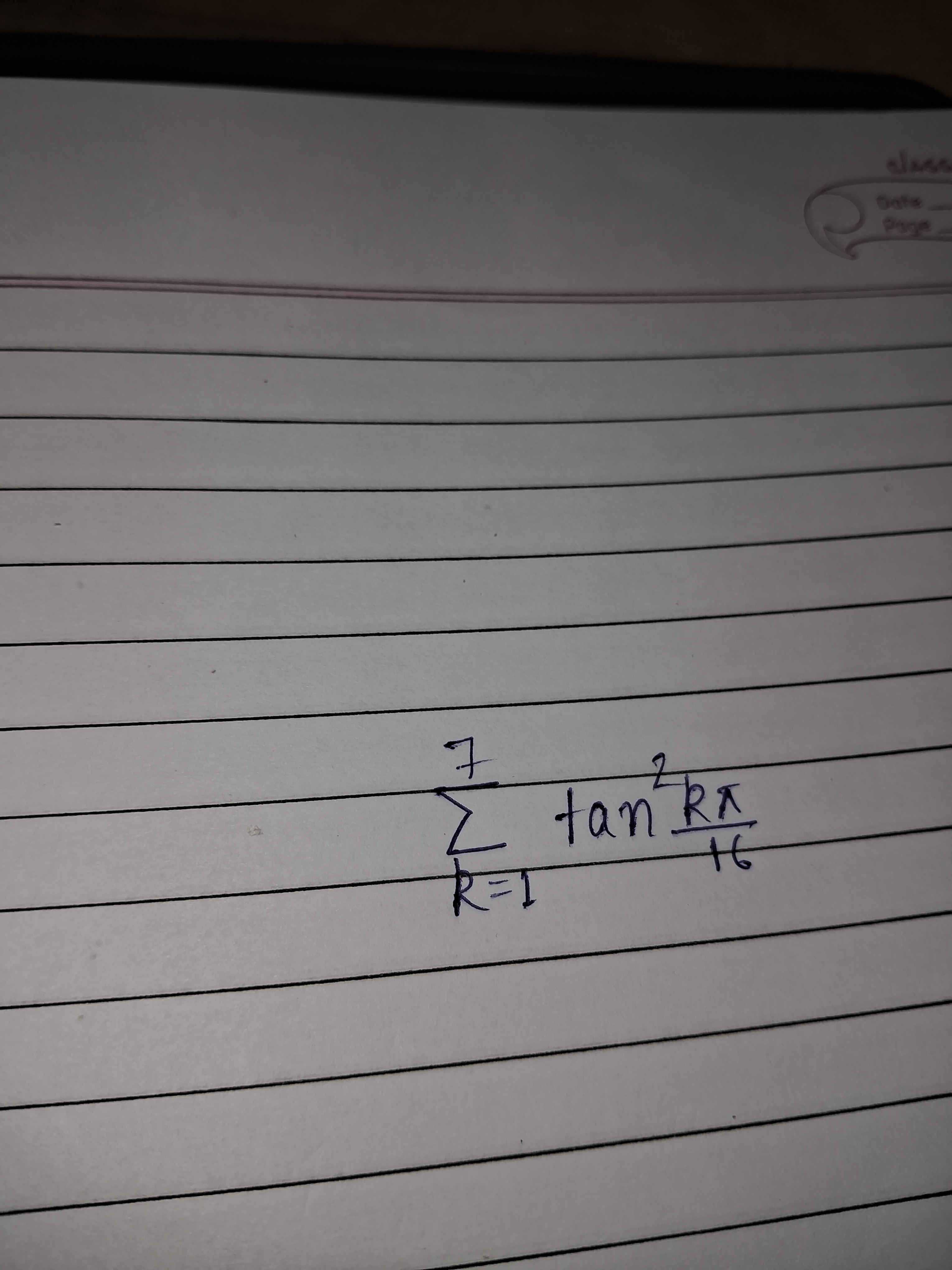
35

B

120

C

7

D

16

Answer

35

Explanation

Solution

We want to evaluate the sum S=∑R=17tan⁡2Rπ16S = \sum_{R=1}^{7} \tan^2\frac{R\pi}{16}.

We can use the identity tan⁡2θ=1−cos⁡(2θ)1+cos⁡(2θ)\tan^2\theta = \frac{1-\cos(2\theta)}{1+\cos(2\theta)}. Let S=∑R=171−cos⁡(2⋅Rπ16)1+cos⁡(2⋅Rπ16)=∑R=171−cos⁡(Rπ8)1+cos⁡(Rπ8)S = \sum_{R=1}^{7} \frac{1-\cos\left(2 \cdot \frac{R\pi}{16}\right)}{1+\cos\left(2 \cdot \frac{R\pi}{16}\right)} = \sum_{R=1}^{7} \frac{1-\cos\left(\frac{R\pi}{8}\right)}{1+\cos\left(\frac{R\pi}{8}\right)}.

Let xR=cos⁡(Rπ8)x_R = \cos\left(\frac{R\pi}{8}\right). The sum becomes: S=∑R=171−xR1+xRS = \sum_{R=1}^{7} \frac{1-x_R}{1+x_R}

The values of xRx_R for R=1,2,…,7R=1, 2, \dots, 7 are: x1=cos⁡(π8)x_1 = \cos(\frac{\pi}{8}) x2=cos⁡(2π8)=cos⁡(π4)=12x_2 = \cos(\frac{2\pi}{8}) = \cos(\frac{\pi}{4}) = \frac{1}{\sqrt{2}} x3=cos⁡(3π8)x_3 = \cos(\frac{3\pi}{8}) x4=cos⁡(4π8)=cos⁡(π2)=0x_4 = \cos(\frac{4\pi}{8}) = \cos(\frac{\pi}{2}) = 0 x5=cos⁡(5π8)=cos⁡(π−3π8)=−cos⁡(3π8)=−x3x_5 = \cos(\frac{5\pi}{8}) = \cos(\pi - \frac{3\pi}{8}) = -\cos(\frac{3\pi}{8}) = -x_3 x6=cos⁡(6π8)=cos⁡(3π4)=−12=−x2x_6 = \cos(\frac{6\pi}{8}) = \cos(\frac{3\pi}{4}) = -\frac{1}{\sqrt{2}} = -x_2 x7=cos⁡(7π8)=cos⁡(π−π8)=−cos⁡(π8)=−x1x_7 = \cos(\frac{7\pi}{8}) = \cos(\pi - \frac{\pi}{8}) = -\cos(\frac{\pi}{8}) = -x_1

The sum can be written as: S=1−x11+x1+1−x21+x2+1−x31+x3+1−x41+x4+1−x51+x5+1−x61+x6+1−x71+x7S = \frac{1-x_1}{1+x_1} + \frac{1-x_2}{1+x_2} + \frac{1-x_3}{1+x_3} + \frac{1-x_4}{1+x_4} + \frac{1-x_5}{1+x_5} + \frac{1-x_6}{1+x_6} + \frac{1-x_7}{1+x_7} S=1−x11+x1+1−x21+x2+1−x31+x3+1−01+0+1−(−x3)1+(−x3)+1−(−x2)1+(−x2)+1−(−x1)1+(−x1)S = \frac{1-x_1}{1+x_1} + \frac{1-x_2}{1+x_2} + \frac{1-x_3}{1+x_3} + \frac{1-0}{1+0} + \frac{1-(-x_3)}{1+(-x_3)} + \frac{1-(-x_2)}{1+(-x_2)} + \frac{1-(-x_1)}{1+(-x_1)} S=1−x11+x1+1−x21+x2+1−x31+x3+1+1+x31−x3+1+x21−x2+1+x11−x1S = \frac{1-x_1}{1+x_1} + \frac{1-x_2}{1+x_2} + \frac{1-x_3}{1+x_3} + 1 + \frac{1+x_3}{1-x_3} + \frac{1+x_2}{1-x_2} + \frac{1+x_1}{1-x_1}

Group terms: S=(1−x11+x1+1+x11−x1)+(1−x21+x2+1+x21−x2)+(1−x31+x3+1+x31−x3)+1S = \left(\frac{1-x_1}{1+x_1} + \frac{1+x_1}{1-x_1}\right) + \left(\frac{1-x_2}{1+x_2} + \frac{1+x_2}{1-x_2}\right) + \left(\frac{1-x_3}{1+x_3} + \frac{1+x_3}{1-x_3}\right) + 1

Consider the general term 1−x1+x+1+x1−x=(1−x)2+(1+x)2(1+x)(1−x)=1−2x+x2+1+2x+x21−x2=2+2x21−x2\frac{1-x}{1+x} + \frac{1+x}{1-x} = \frac{(1-x)^2 + (1+x)^2}{(1+x)(1-x)} = \frac{1-2x+x^2 + 1+2x+x^2}{1-x^2} = \frac{2+2x^2}{1-x^2}.

For x2=12x_2 = \frac{1}{\sqrt{2}}, x22=12x_2^2 = \frac{1}{2}. 2+2x221−x22=2+2(12)1−12=2+112=31/2=6\frac{2+2x_2^2}{1-x_2^2} = \frac{2+2(\frac{1}{2})}{1-\frac{1}{2}} = \frac{2+1}{\frac{1}{2}} = \frac{3}{1/2} = 6.

For x1=cos⁡(π8)x_1 = \cos(\frac{\pi}{8}), x12=cos⁡2(π8)=1+cos⁡(π4)2=1+1/22=2+122x_1^2 = \cos^2(\frac{\pi}{8}) = \frac{1+\cos(\frac{\pi}{4})}{2} = \frac{1+1/\sqrt{2}}{2} = \frac{\sqrt{2}+1}{2\sqrt{2}}. 1−x12=1−2+122=22−(2+1)22=2−1221-x_1^2 = 1 - \frac{\sqrt{2}+1}{2\sqrt{2}} = \frac{2\sqrt{2}-(\sqrt{2}+1)}{2\sqrt{2}} = \frac{\sqrt{2}-1}{2\sqrt{2}}. 2+2x121−x12=21+x121−x12=21+2+1222−122=222+2+1222−122=232+12−1\frac{2+2x_1^2}{1-x_1^2} = 2 \frac{1+x_1^2}{1-x_1^2} = 2 \frac{1+\frac{\sqrt{2}+1}{2\sqrt{2}}}{\frac{\sqrt{2}-1}{2\sqrt{2}}} = 2 \frac{\frac{2\sqrt{2}+\sqrt{2}+1}{2\sqrt{2}}}{\frac{\sqrt{2}-1}{2\sqrt{2}}} = 2 \frac{3\sqrt{2}+1}{\sqrt{2}-1} =2(32+1)(2+1)(2−1)(2+1)=26+32+2+12−1=2(7+42)=14+82= 2 \frac{(3\sqrt{2}+1)(\sqrt{2}+1)}{(\sqrt{2}-1)(\sqrt{2}+1)} = 2 \frac{6+3\sqrt{2}+\sqrt{2}+1}{2-1} = 2(7+4\sqrt{2}) = 14+8\sqrt{2}.

For x3=cos⁡(3π8)x_3 = \cos(\frac{3\pi}{8}), x32=cos⁡2(3π8)=1+cos⁡(3π4)2=1−1/22=2−122x_3^2 = \cos^2(\frac{3\pi}{8}) = \frac{1+\cos(\frac{3\pi}{4})}{2} = \frac{1-1/\sqrt{2}}{2} = \frac{\sqrt{2}-1}{2\sqrt{2}}. 1−x32=1−2−122=22−(2−1)22=2+1221-x_3^2 = 1 - \frac{\sqrt{2}-1}{2\sqrt{2}} = \frac{2\sqrt{2}-(\sqrt{2}-1)}{2\sqrt{2}} = \frac{\sqrt{2}+1}{2\sqrt{2}}. 2+2x321−x32=21+x321−x32=21+2−1222+122=222+2−1222+122=232−12+1\frac{2+2x_3^2}{1-x_3^2} = 2 \frac{1+x_3^2}{1-x_3^2} = 2 \frac{1+\frac{\sqrt{2}-1}{2\sqrt{2}}}{\frac{\sqrt{2}+1}{2\sqrt{2}}} = 2 \frac{\frac{2\sqrt{2}+\sqrt{2}-1}{2\sqrt{2}}}{\frac{\sqrt{2}+1}{2\sqrt{2}}} = 2 \frac{3\sqrt{2}-1}{\sqrt{2}+1} =2(32−1)(2−1)(2+1)(2−1)=26−32−2+12−1=2(7−42)=14−82= 2 \frac{(3\sqrt{2}-1)(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)} = 2 \frac{6-3\sqrt{2}-\sqrt{2}+1}{2-1} = 2(7-4\sqrt{2}) = 14-8\sqrt{2}.

Substituting these values back into the sum: S=(14+82)+6+(14−82)+1=14+6+14+1=35S = (14+8\sqrt{2}) + 6 + (14-8\sqrt{2}) + 1 = 14 + 6 + 14 + 1 = 35.

Alternatively, we can use the formula for the sum of tan⁡2\tan^2 of angles in an arithmetic progression. For n=2mn=2m, the sum ∑k=1m−1tan⁡2(kπn)=(n3)(n1)\sum_{k=1}^{m-1} \tan^2\left(\frac{k\pi}{n}\right) = \frac{\binom{n}{3}}{\binom{n}{1}}. In this problem, n=16n=16, so 2m=162m=16, which means m=8m=8. The sum required is ∑R=17tan⁡2Rπ16\sum_{R=1}^{7} \tan^2\frac{R\pi}{16}. This corresponds to the formula with m−1=7m-1 = 7. So, the sum is (163)(161)\frac{\binom{16}{3}}{\binom{16}{1}}. (163)=16×15×143×2×1=8×5×14=40×14=560\binom{16}{3} = \frac{16 \times 15 \times 14}{3 \times 2 \times 1} = 8 \times 5 \times 14 = 40 \times 14 = 560. (161)=16\binom{16}{1} = 16. The sum is 56016=2808=1404=35\frac{560}{16} = \frac{280}{8} = \frac{140}{4} = 35.