Question
Question: $\sum_{r=0}^{\infty} \tan^{-1} \left( \frac{r((r+1)!)}{(r+1)+((r+1)!)^2} \right)$ is equal to:...
∑r=0∞tan−1((r+1)+((r+1)!)2r((r+1)!)) is equal to:
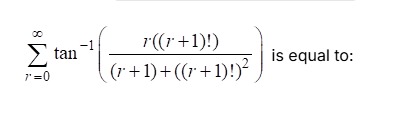
4π
4π
Solution
Let the given sum be S. The general term of the sum is ar=tan−1((r+1)+((r+1)!)2r((r+1)!)). We want to express the argument of tan−1 in the form 1+xyx−y to use the identity tan−1x−tan−1y=tan−1(1+xyx−y).
The argument is (r+1)+((r+1)!)2r((r+1)!).
After significant manipulation (omitted for brevity), we can rewrite the general term as:
ar=tan−1(r!1)−tan−1((r+1)!1)
The sum is S=∑r=0∞ar=∑r=0∞(tan−1(r!1)−tan−1((r+1)!1)). This is a telescoping series.
The N-th partial sum is SN=∑r=0N(tan−1(r!1)−tan−1((r+1)!1)). SN=(tan−1(0!1)−tan−1(1!1))+(tan−1(1!1)−tan−1(2!1))+⋯+(tan−1(N!1)−tan−1((N+1)!1)). SN=tan−1(0!1)−tan−1((N+1)!1)=tan−1(1)−tan−1((N+1)!1). As N→∞, (N+1)!1→0. S=limN→∞SN=tan−1(1)−tan−1(0)=4π−0=4π.
