Question

$\sum_{n=1}^{\infty}\sum_{k=1}^{n-1}\frac{k}{2^{n+k}}$ is equal to -

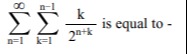
• A. 1/9
• B. 2/9
• C. 4/9
• D. 5/9

Answer 1

Answer: (C)

4/9

Answer 2

The given double summation is $S = \sum_{n=1}^{\infty}\sum_{k=1}^{n-1}\frac{k}{2^{n+k}}$. The summation region is $1 \le k \le n-1$ for $n \ge 1$. This implies $n \ge 2$.

We swap the order of summation. The region is $k \ge 1$ and $n \ge k+1$.

The sum becomes $\sum_{k=1}^{\infty}\sum_{n=k+1}^{\infty}\frac{k}{2^n 2^k}$.

The inner sum is a geometric series $\sum_{n=k+1}^{\infty}\frac{1}{2^n} = \frac{1/2^{k+1}}{1-1/2} = \frac{1}{2^k}$.

The outer sum becomes $\sum_{k=1}^{\infty}\frac{k}{2^k} \cdot \frac{1}{2^k} = \sum_{k=1}^{\infty}\frac{k}{4^k}$.

This is an arithmetic-geometric series $\sum_{k=1}^{\infty} kr^k$ with $r=1/4$.

The sum is $\frac{r}{(1-r)^2} = \frac{1/4}{(1-1/4)^2} = \frac{1/4}{(3/4)^2} = \frac{1/4}{9/16} = \frac{4}{9}$.

The final answer is $\frac{4}{9}$.