Question
Question: $\sum_{n=1}^{\infty}\frac{1}{n!}=?$...
∑n=1∞n!1=?
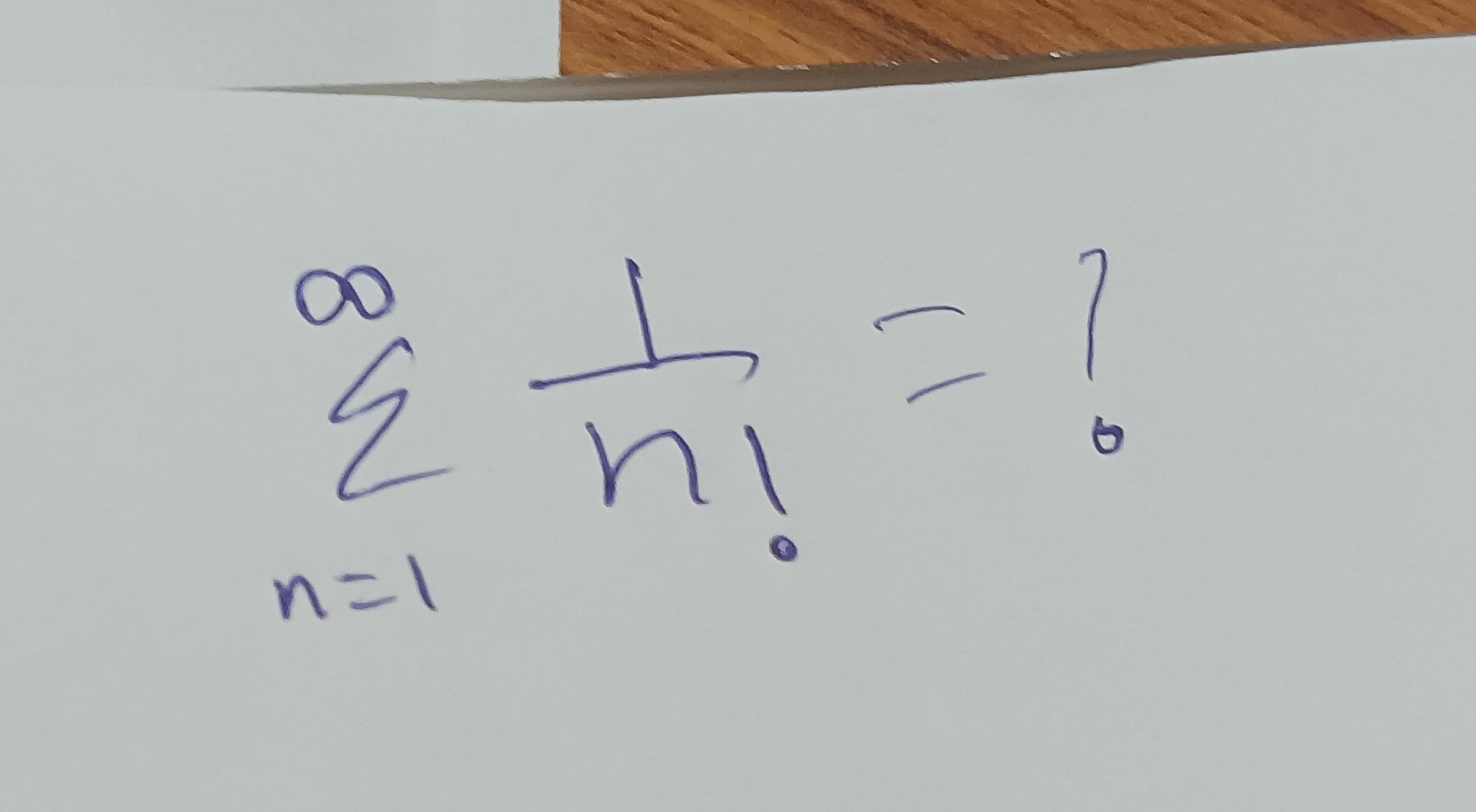
Answer
e-1
Explanation
Solution
The problem asks for the sum of the infinite series ∑n=1∞n!1.
We know the Maclaurin series expansion for ex is given by: ex=∑n=0∞n!xn=0!x0+1!x1+2!x2+3!x3+… Substitute x=1 into this series: e1=e=∑n=0∞n!1n=∑n=0∞n!1 Expanding the sum for e: e=0!1+1!1+2!1+3!1+… Since 0!=1, we can write: e=1+1!1+2!1+3!1+… The given series is ∑n=1∞n!1=1!1+2!1+3!1+…. Comparing this with the expansion of e, we can see that: e=1+(1!1+2!1+3!1+…) e=1+∑n=1∞n!1 To find the value of the given series, we rearrange the equation: ∑n=1∞n!1=e−1
