Question
Question: $\sum_{h=1}^{n} \frac{cos(3n+1)x - cos(3n+2)}{1+2cos(2n+1)x}$...
∑h=1n1+2cos(2n+1)xcos(3n+1)x−cos(3n+2)
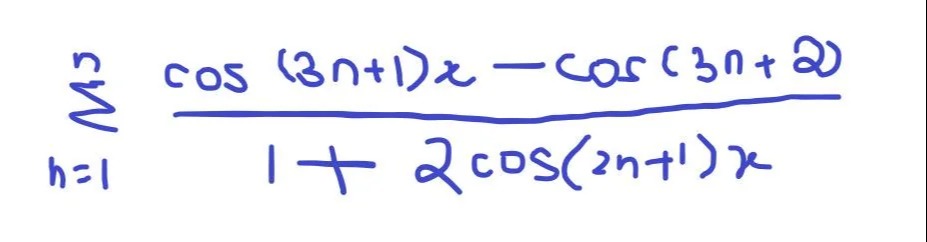
Answer
21[tan2(2n+1)x−tan2x]
Explanation
Solution
Rewrite the numerator using the cosine subtraction formula and express it, along with the denominator, in a form that can be written as the difference of two tangents divided by 2. The sum telescopes, leaving only the first and last terms.
