Question
Question: $\sum_{\gamma=0}^{n} \frac{(-1)^{\gamma}}{^{n}C_{\gamma}}$...
∑γ=0nnCγ(−1)γ
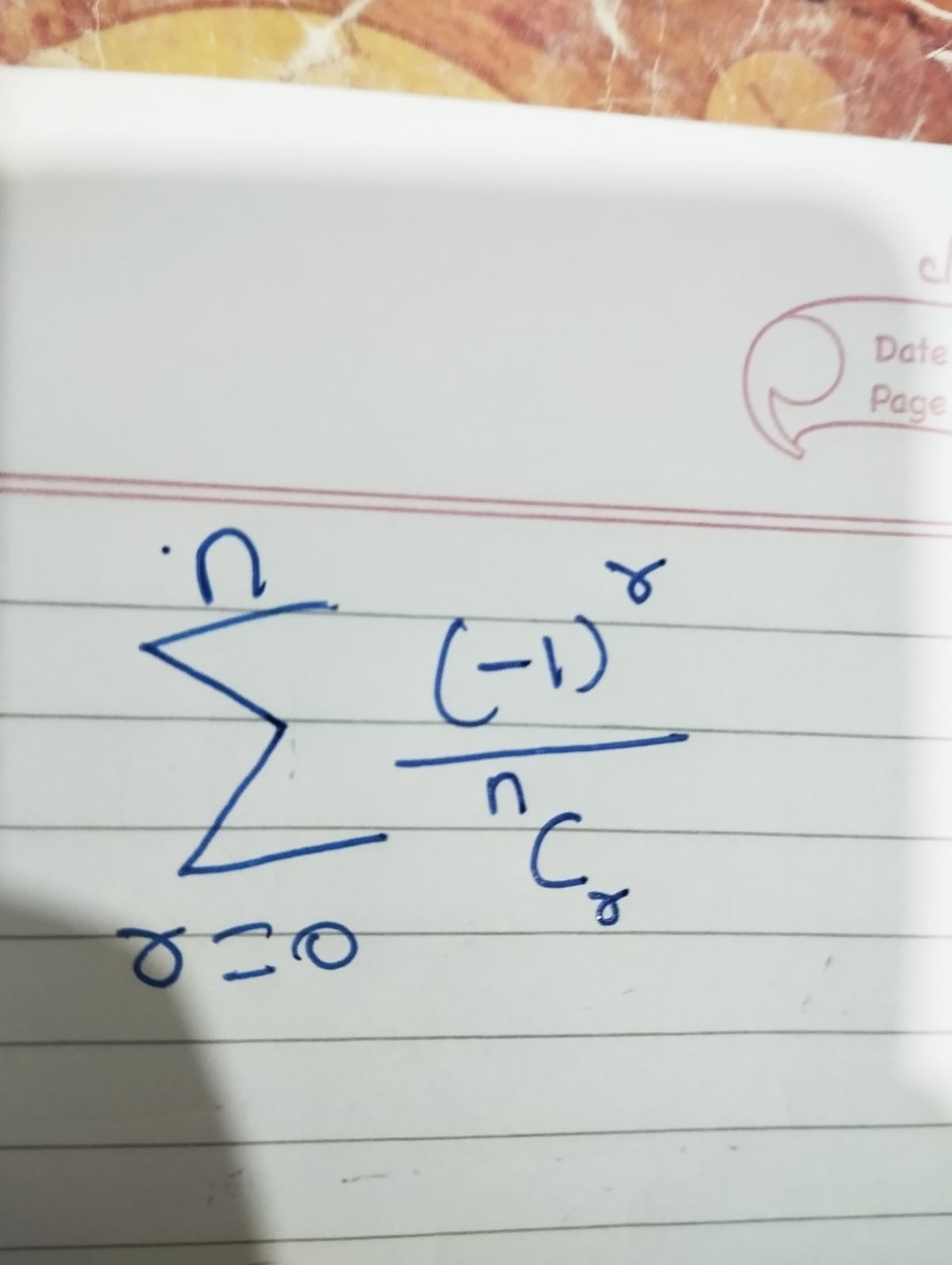
{0,n+22(n+1),if n is odd,if n is even.
Solution
We want to evaluate
S(n)=∑γ=0n(γn)(−1)γ.
Step 1. Rewrite the summation:
Recall that
(γn)=γ!(n−γ)!n!⟹(γn)1=n!γ!(n−γ)!.
Thus,
S(n)=∑γ=0n(−1)γn!γ!(n−γ)!.
Step 2. Convert into an Integral Using the Beta Function:
Notice that
∫01xγ(1−x)n−γdx=(n+1)!γ!(n−γ)!.
This implies
n!γ!(n−γ)!=(n+1)∫01xγ(1−x)n−γdx.
Thus, we can write
S(n)=(n+1)∫01[∑γ=0n(−1)γxγ(1−x)n−γ]dx.
Step 3. Evaluate the Sum inside the Integral:
Note that
(1−x)n−γxγ=(1−x)n(1−xx)γ.
So the inner summation becomes
∑γ=0n(−1)γ(1−xx)γ=(1−x)⋅1−x+x1−(−1−xx)n+1
since
1+1−xx=1−x1.
In fact, a simpler way is to recognize it as a finite geometric series: Let
r=−1−xx.
Then
∑γ=0nrγ=1−r1−rn+1.
Substituting back, we have
∑γ=0n(−1)γ(1−xx)γ=1+1−xx1−(−1−xx)n+1=(1−x)[1−(−1)n+1(1−xx)n+1].
Thus the inner expression becomes
(1−x)n⋅(1−x)[1−(−1)n+1(1−xx)n+1]=(1−x)n+1[1−(−1)n+1(1−x)n+1xn+1].
That is,
(1−x)n+1−(−1)n+1xn+1.
Step 4. Complete the Integral:
So
S(n)=(n+1)∫01[(1−x)n+1−(−1)n+1xn+1]dx.
We now evaluate the integrals separately:
-
∫01(1−x)n+1dx=n+21.
-
∫01xn+1dx=n+21.
Thus,
S(n)=(n+1)[n+21−(−1)n+1n+21]=n+2n+1[1−(−1)n+1].
Step 5. Write the Final Answer According to the Parity of n:
- If n is odd then n+1 is even so (−1)n+1=1 and
S(n)=n+2n+1[1−1]=0.
- If n is even then n+1 is odd so (−1)n+1=−1 and
S(n)=n+2n+1[1−(−1)]=n+22(n+1).
