Question

$\sum_{1}^{45} \frac{1}{sin(2n-1)}$

Answer 1

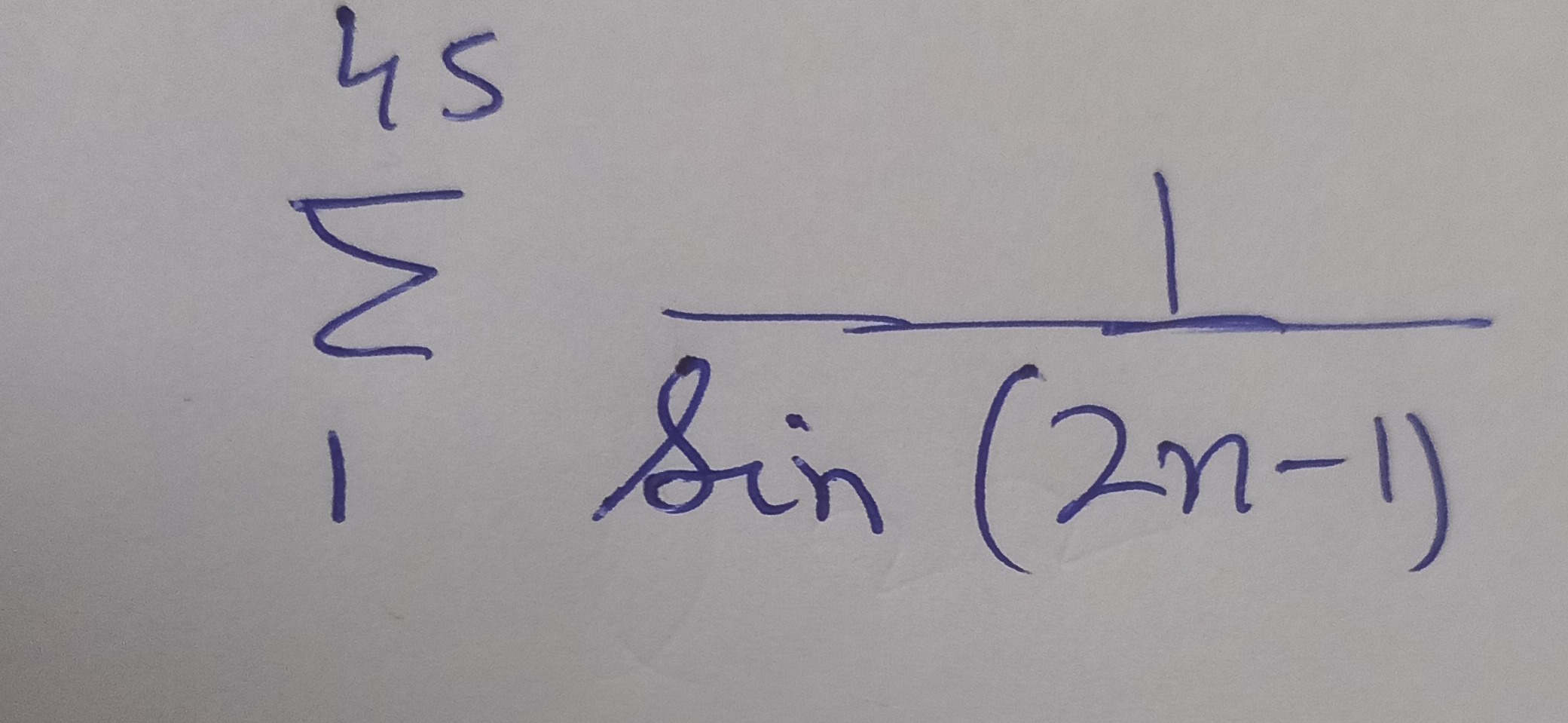
The problem likely contains a typo and should be $\sum_{n=1}^{45} \frac{1}{\sin(2n-1)^\circ \sin(2n+1)^\circ}$, which evaluates to $\frac{2}{\sin^2(2^\circ)}$.

Answer 2

The problem as stated, $\sum_{n=1}^{45} \frac{1}{\sin(2n-1)}$, involves a sum of reciprocals of sines of angles in an arithmetic progression ($1^\circ, 3^\circ, \dots, 89^\circ$). This sum does not have a simple closed form that can be derived using standard techniques typically taught for JEE/NEET.

It is highly probable that there is a typo in the question, and it is intended to be a telescoping sum, which is a common type of problem in competitive exams. The most common form for such sums involving trigonometric functions is $\sum \frac{1}{\sin A \sin B}$ or similar.

Let's assume the question is intended to be: $S = \sum_{n=1}^{45} \frac{1}{\sin(2n-1)^\circ \sin(2n+1)^\circ}$ This assumption leads to a solvable telescoping series.

Steps to solve with the assumed correction:

1. Analyze the general term: The general term is $T_n = \frac{1}{\sin(2n-1)^\circ \sin(2n+1)^\circ}$. The angles in the denominator are in an arithmetic progression with a common difference of $2^\circ$.

2. Apply the telescoping sum technique: We use the identity $\sin(A-B) = \sin A \cos B - \cos A \sin B$. Consider the term $\frac{\sin((2n+1)^\circ - (2n-1)^\circ)}{\sin(2n-1)^\circ \sin(2n+1)^\circ}$. The numerator is $\sin(2^\circ)$. So, we can write $T_n$ as: $T_n = \frac{1}{\sin(2^\circ)} \cdot \frac{\sin((2n+1)^\circ - (2n-1)^\circ)}{\sin(2n-1)^\circ \sin(2n+1)^\circ}$ $T_n = \frac{1}{\sin(2^\circ)} \cdot \frac{\sin(2n+1)^\circ \cos(2n-1)^\circ - \cos(2n+1)^\circ \sin(2n-1)^\circ}{\sin(2n-1)^\circ \sin(2n+1)^\circ}$ $T_n = \frac{1}{\sin(2^\circ)} \left( \frac{\cos(2n-1)^\circ}{\sin(2n-1)^\circ} - \frac{\cos(2n+1)^\circ}{\sin(2n+1)^\circ} \right)$ $T_n = \frac{1}{\sin(2^\circ)} (\cot(2n-1)^\circ - \cot(2n+1)^\circ)$

3. Sum the terms: Now, we sum $T_n$ from $n=1$ to $45$: $S = \sum_{n=1}^{45} \frac{1}{\sin(2^\circ)} (\cot(2n-1)^\circ - \cot(2n+1)^\circ)$ $S = \frac{1}{\sin(2^\circ)} \sum_{n=1}^{45} (\cot(2n-1)^\circ - \cot(2n+1)^\circ)$ This is a telescoping sum: For $n=1$: $\cot(1^\circ) - \cot(3^\circ)$ For $n=2$: $\cot(3^\circ) - \cot(5^\circ)$ For $n=3$: $\cot(5^\circ) - \cot(7^\circ)$ ... For $n=45$: $\cot(2 \times 45 - 1)^\circ - \cot(2 \times 45 + 1)^\circ = \cot(89^\circ) - \cot(91^\circ)$

   Adding these terms, all intermediate terms cancel out: $\sum_{n=1}^{45} (\cot(2n-1)^\circ - \cot(2n+1)^\circ) = \cot(1^\circ) - \cot(91^\circ)$

4. Simplify the result: We know that $\cot(90^\circ + \theta) = -\tan(\theta)$. So, $\cot(91^\circ) = \cot(90^\circ + 1^\circ) = -\tan(1^\circ)$. The sum inside the bracket becomes: $\cot(1^\circ) - (-\tan(1^\circ)) = \cot(1^\circ) + \tan(1^\circ)$ Using the identity $\cot \theta + \tan \theta = \frac{\cos \theta}{\sin \theta} + \frac{\sin \theta}{\cos \theta} = \frac{\cos^2 \theta + \sin^2 \theta}{\sin \theta \cos \theta} = \frac{1}{\sin \theta \cos \theta}$. So, $\cot(1^\circ) + \tan(1^\circ) = \frac{1}{\sin(1^\circ) \cos(1^\circ)}$. We also know that $\sin(2\theta) = 2 \sin \theta \cos \theta$, so $\sin \theta \cos \theta = \frac{\sin(2\theta)}{2}$. Thus, $\frac{1}{\sin(1^\circ) \cos(1^\circ)} = \frac{1}{\frac{\sin(2^\circ)}{2}} = \frac{2}{\sin(2^\circ)}$.

5. Final Answer: Substitute this back into the expression for $S$: $S = \frac{1}{\sin(2^\circ)} \times \frac{2}{\sin(2^\circ)} = \frac{2}{\sin^2(2^\circ)}$

Given the nature of competitive exams, the most plausible interpretation of the question is that it was intended to be a telescoping sum of the form $\sum \frac{1}{\sin A \sin B}$.